Bicubic Interpolation

이 보간법은 $(x, y)|0 \le x \le 1, 0 \le y \le 1$로 정의되는 $D$의 임의의 점 $x, y$로 부터 16개의 점의 값을 보간하는 방법이다.

 

보간 곡면 $f(x, y)$는 다음과 같이 $x, y$의 3차 함수로 정의된다.

 

$f(x, y) = \sum_{i=0}^3 \sum_{j=0}^3 a_{ij} x^i y^j$

 

보간하는 점이 16개인 이유는 위의 수식에서 미지수가 $a_{00}$ ~ $a_{33}$으로 16개이기 때문이다. 미지수가 16개이기 때문에 자명한 해를 구하기 위해서는 16개의 관계식이 필요하다. 따라서 계수를 추정하기 위해 $D$의 4개의 코너에 대한 함수값, x에 대한 편미분, y에 대한 편미분, 그리고 x, y에 대한 편미분을 사용한다.

 

먼저 4개의 코너에 대한 함수값은 다음과 같다.

 

x에 대한 편미분, y에 대한 편미분 값은 다음과 같다.

 

마지막으로 x, y에 대한 편미분 값은 다음과 같다.

 

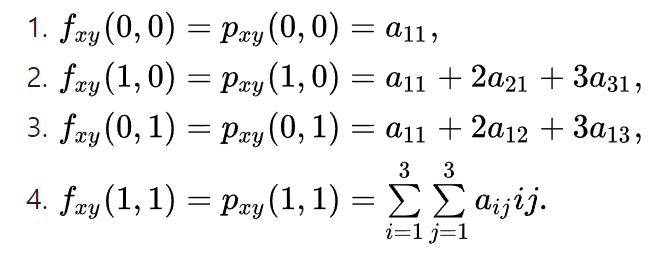
우리가 찾고자 하는 계수를 벡터 $\alpha$를 다음과 같이 정의할 수 있다.

 

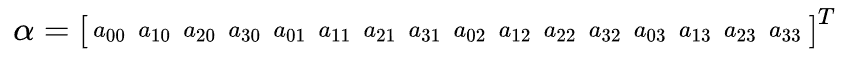
그리고 임의의 점 $x, y$로 부터의 함수값과 편미분 값을 다음과 같이 벡터 $x$로 정의할 수 있다.

 

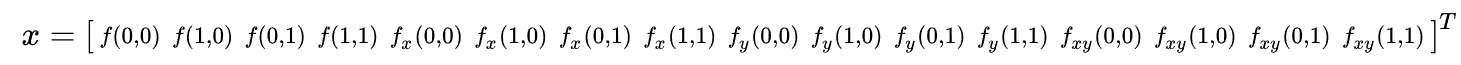
위의 16개의 수식으로 부터 $A \alpha = x$를 만족하는 $A$를 정의할 수 있고, 찾고자 하는 $\alpha$는 $A^{-1}x = \alpha$로 계산할 수 있다.

 

$A^{-1}$는 다음과 같이 정의된다.

 

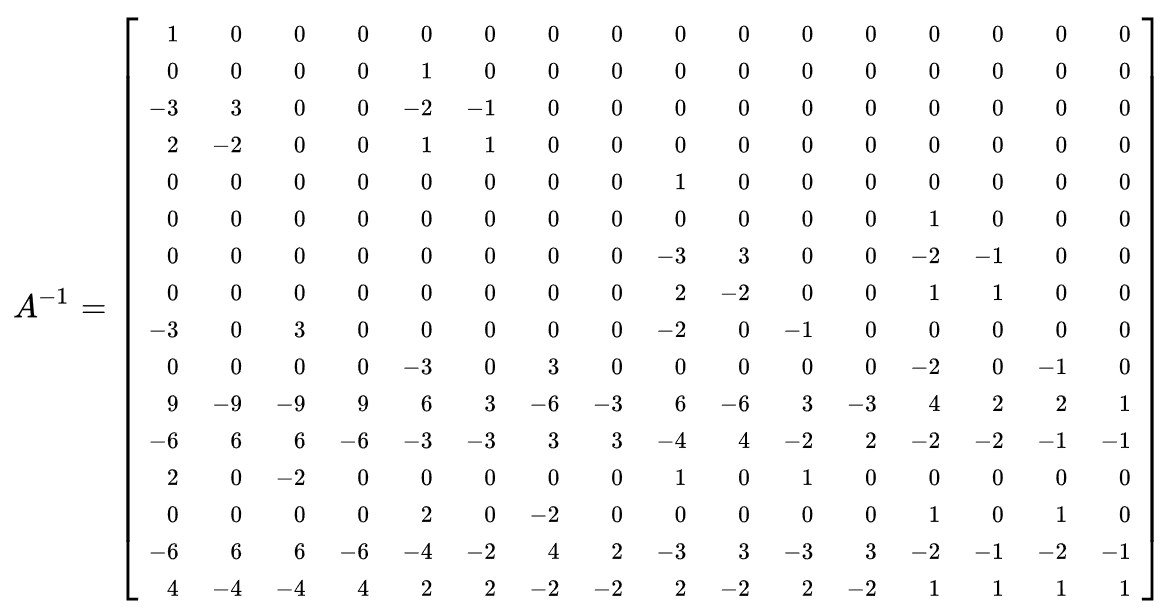
실제로 이미지 처리나 딥러닝을 위해 계산 할 때는 위와 같이 거대한 행렬을 만들지 않고 bicubic convolution algorithm을 적용해 계산한다고 한다.