1. Linear Regression을 분류에 적용할 때 문제점

- 회귀식은 생성된 값에 제한이 없다. 위 그림의 왼쪽 선형 회귀 그래프를 보면 결과값이 0 미만 혹은 1 초과 값도 생성될 수 있어서 문제가 발생한다.
- 그러나 이진 분류에서는 오직 0과 1 두 가지 결괏값만 가능하다.
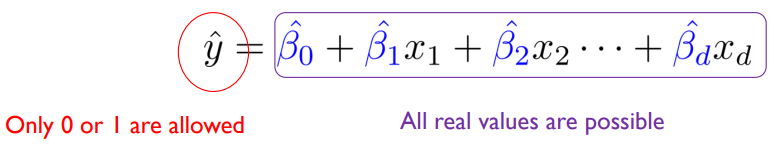
따라서 위의 선형 회귀 식을 분류에 적용하려고 하면 독립변수와 종속변수의 범위가 일치하지 않는 문제가 생긴다.
이러한 문제를 해결하면서 회귀 모델의 장점을 계승하는 분류 모델을 만들어야 한다. 회귀 모델의 장점이란 중요한 변수를 찾는 능력과 설명력을 의미한다.
2. Logistic Regression
목표 : 0/1 결과와 관련된 예측 변수의 함수를 찾는다.
- Y를 결과 변수로 사용하는 대신(선형 회귀 분석처럼) "logit"이라는 Y에 대한 함수를 사용한다.
- Logit은 예측 변수의 선형 함수로 모델링될 수 있다.
- Logit은 확률에 다시 매핑될 수 있으며, 이는 다시 클래스에 매핑될 수 있다.
2.1 Odds
스포츠 경기의 배팅 확률 등은 다음과 같이 표현되어 있다.

odds는 (성공할 확률/성공하지 못할 확률)로써 다음과 같이 계산한다.

가령 스페인을 예로 들면 $\frac {p}{1-p} = \frac {2}{9}$라서 스페인이 우승할 확률은 $p=2/11$로 계산할 수 있다.
odds의 범위는 $[0, \infty)$이고 그래프는 다음과 같다.
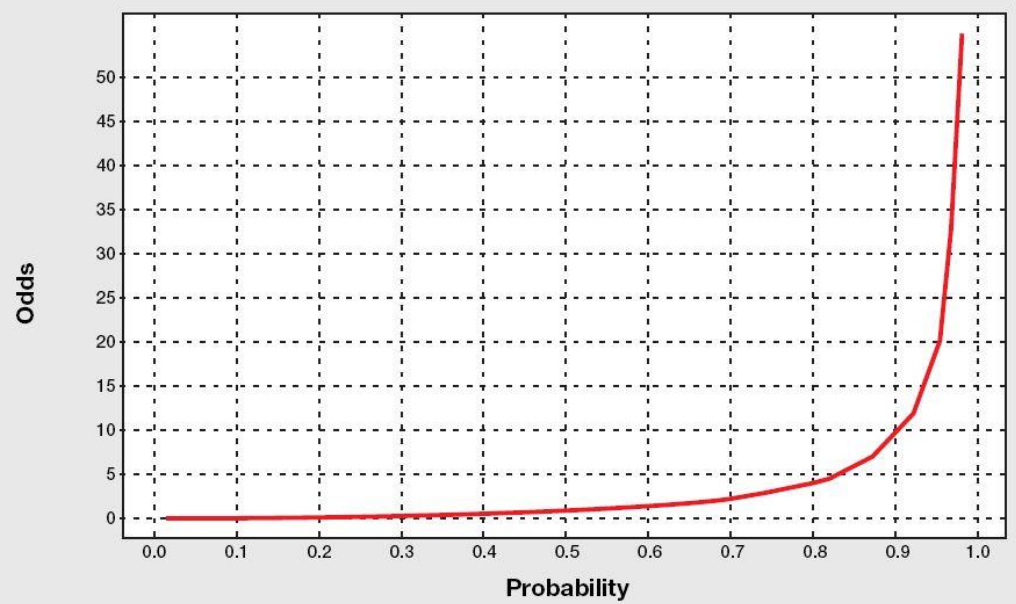
odds의 단점은 다음과 같다.
- 음수가 불가능
- 비대칭
그래서 odds에 자연 로그를 씌워서 사용한다.
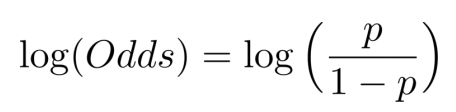
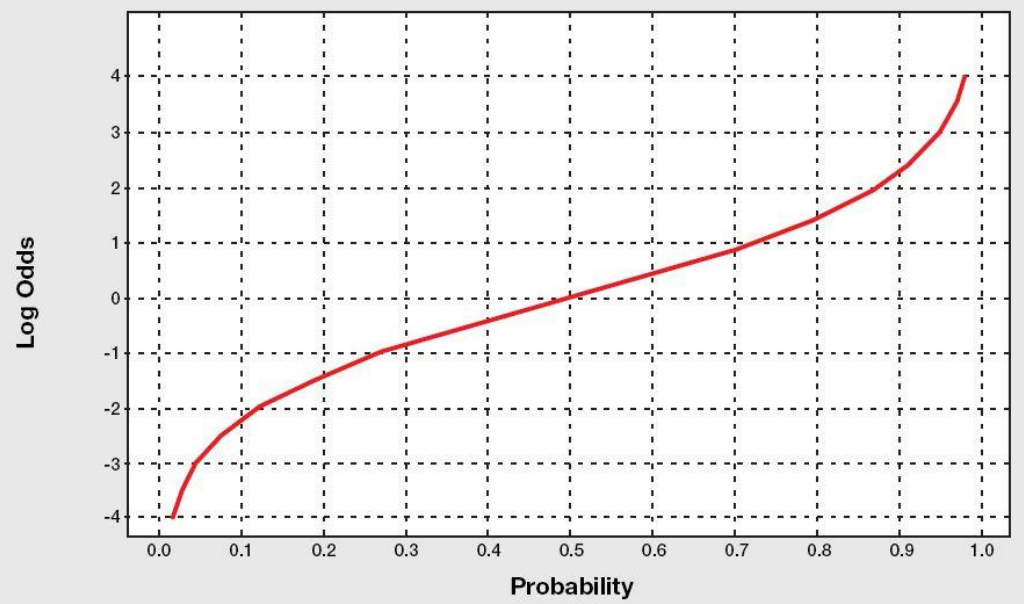
이렇게하면 음의 무한대에서 양의 무한대의 범위를 갖는다. 그래프 또한 대칭이다.
2.2 Equation
독립변수와 종속변수의 범위를 일치시킨 odds를 사용한 선형 방정식은 다음과 같다.
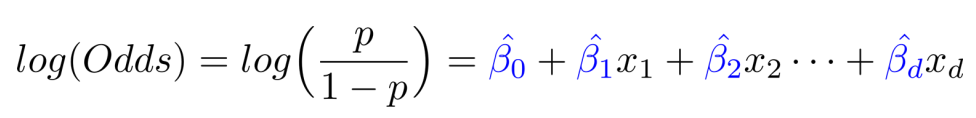
양변에 exponetial을 적용하면 다음과 같다.
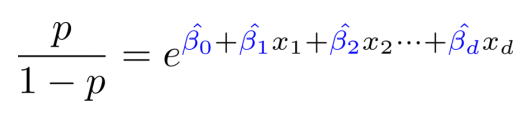
확률 p에 대해서 정리하면 다음과 같이 Logistic regression의 수식이 유도된다.
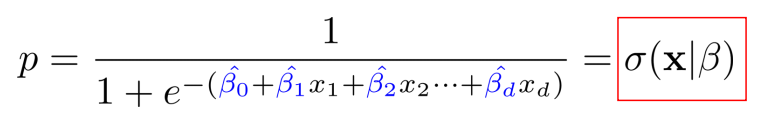
'Machine Learning > Business Analytics 1' 카테고리의 다른 글
| Logistic Regression : Interpretation (0) | 2023.12.20 |
|---|---|
| Logistic Regression : Learning (0) | 2023.12.19 |
| Evaluating Regression Models (0) | 2023.12.08 |
| Multiple Linear Regression (0) | 2023.12.08 |
| Decision Tree (0) | 2023.12.04 |



