LSTM 구현
이전에 보았던 LSTM의 계산 그래프는 다음과 같다.

그리고 아래 수식들은 LSTM에서 수행하는 계산을 정리한 수식들이다.



행렬 라이브러리는 큰 행렬을 한꺼번에 계산할 때 효율이 좋기 때문에 $x{W_x}+h{W_h}+b$ 같은 아핀 변환을 다음과 같이 한 번에 처리한다.

이때의 계산 그래프는 slice 노드를 포함하여 다음과 같이 표현할 수 있다.

이제 LSTM 클래스를 구현해보자. 우선 초기화 부분이다.
class LSTM:
def __init__(self, Wx, Wh, b):
'''
Parameters
----------
Wx: 입력 x에 대한 가중치 매개변수(4개분의 가중치가 담겨 있음)
Wh: 은닉 상태 h에 대한 가장추 매개변수(4개분의 가중치가 담겨 있음)
b: 편향(4개분의 편향이 담겨 있음)
'''
self.params = [Wx, Wh, b]
self.grads = [np.zeros_like(Wx), np.zeros_like(Wh), np.zeros_like(b)]
self.cache = Nonecache에는 역변환에 필요한 것들을 저장해놓는다. forward는 다음과 같다.
def forward(self, x, h_prev, c_prev):
Wx, Wh, b = self.params
N, H = h_prev.shape
A = np.dot(x, Wx) + np.dot(h_prev, Wh) + b
f = A[:, :H]
g = A[:, H:2*H]
i = A[:, 2*H:3*H]
o = A[:, 3*H:]
f = sigmoid(f)
g = np.tanh(g)
i = sigmoid(i)
o = sigmoid(o)
c_next = f * c_prev + g * i
h_next = o * np.tanh(c_next)
self.cache = (x, h_prev, c_prev, i, f, g, o, c_next)
return h_next, c_nextA에 아핀변환을 수행한 결과를 저장해놓고 슬라이싱을 통해 f, g, i, o로 분할한다. 그런 다음 위에서 보았던 수식을 계산하고 hidden state와 메모리셀을 리턴한다.
forward에서 슬라이싱을 수행했기 때문에 backward에서는 이의 반대로 행렬들을 결합해준다. 그림으로 보면 다음과 같다.

backward 구현은 다음과 같다.
def backward(self, dh_next, dc_next):
Wx, Wh, b = self.params
x, h_prev, c_prev, i, f, g, o, c_next = self.cache
tanh_c_next = np.tanh(c_next)
ds = dc_next + (dh_next * o) * (1 - tanh_c_next ** 2)
dc_prev = ds * f
di = ds * g
df = ds * c_prev
do = dh_next * tanh_c_next
dg = ds * i
di *= i * (1 - i)
df *= f * (1 - f)
do *= o * (1 - o)
dg *= (1 - g ** 2)
dA = np.hstack((df, dg, di, do))
dWh = np.dot(h_prev.T, dA)
dWx = np.dot(x.T, dA)
db = dA.sum(axis=0)
self.grads[0][...] = dWx
self.grads[1][...] = dWh
self.grads[2][...] = db
dx = np.dot(dA, Wx.T)
dh_prev = np.dot(dA, Wh.T)
return dx, dh_prev, dc_prev- ds는 '+ 노드'를 지나기 전의 기울기 값을 계산한 것이다.
- 넘파이의 hstack 메서드를 사용해 행렬들을 결합해준다.
LSTM을 사용한 언어모델
5장에서 보았던 것과 유일한 차이는 TimeRNN이 TimeLSTM으로 바뀐 것이다.

rnnlm 구현은 생략하고 추가 개선 부분만 알아보자.
LSTM 계층 다층화
affine 계층을 여러개 쌓는 것 처럼 LSTM 또한 여러 계층을 쌓아 효과를 볼 수 있다. 몇 층을 쌓아야 할지는 튜닝을 통해 결정해야 한다.
드롭아웃에 의한 과적합 억제
RNN은 일반적인 피드포워드 신경망보다 쉽게 과적합을 일으킨다는 단점이 있다. 여러 계층을 쌓는다면 과적합이 더 잘 일어날 것이다. 피드포워드 신경망에 드롭아웃을 적용했던 것 처럼 RNN을 사용한 모델에도 드롭아웃을 적용할 수 있다.
드롭아웃을 적용할 때 시계열 방향으로 적용하면 학습 시 시간이 흐름에 따라 정보가 사라질 수 있다. 따라서 계층(깊이) 방향을 드롭아웃을 적용하는 것이 적절하다.
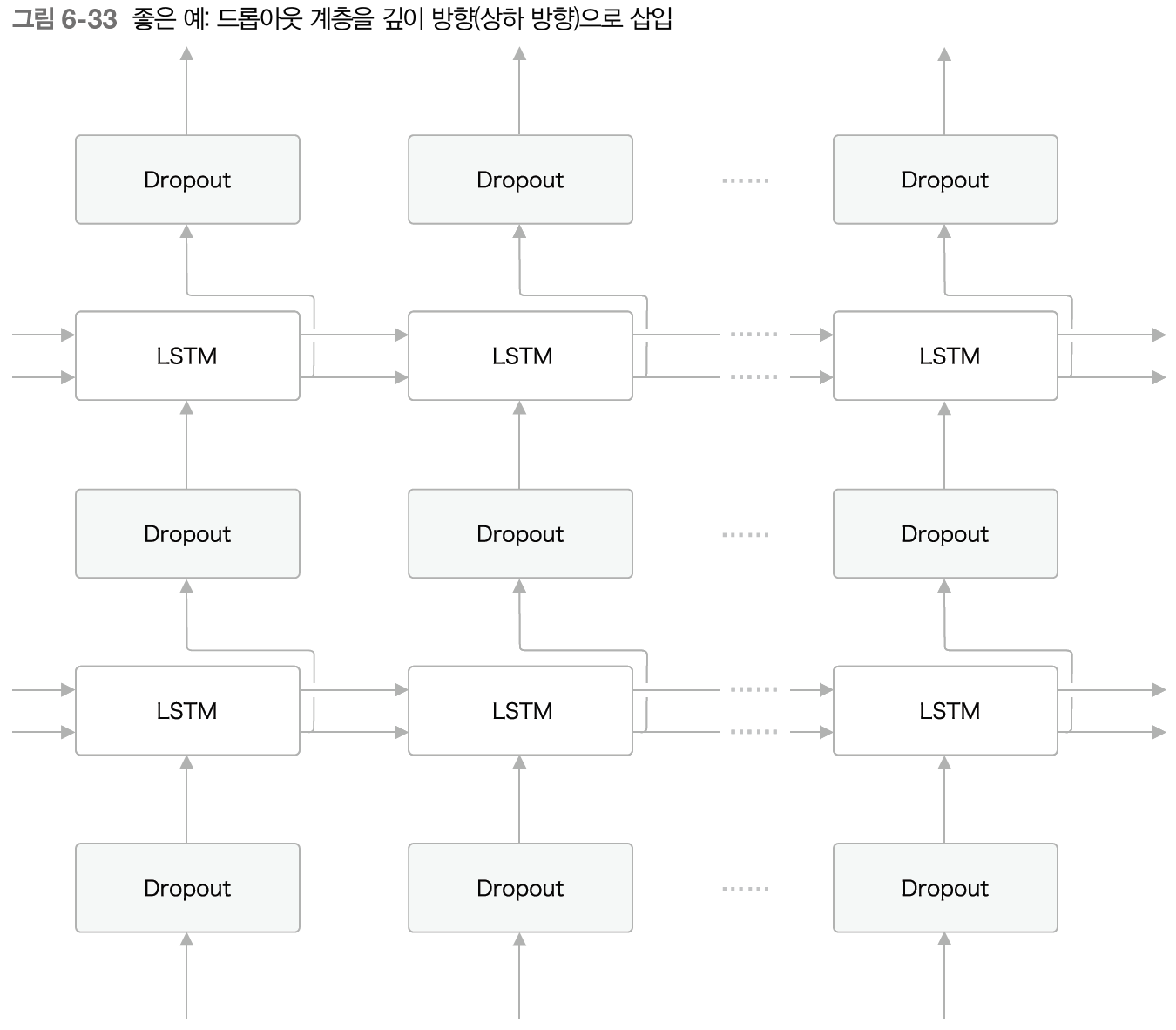
그렇지만 드롭아웃 계층끼리 같은 masking을 공유한다면 시간 방향으로 적용할 수 있다. 이를 변형 드롭아웃이라 한다.
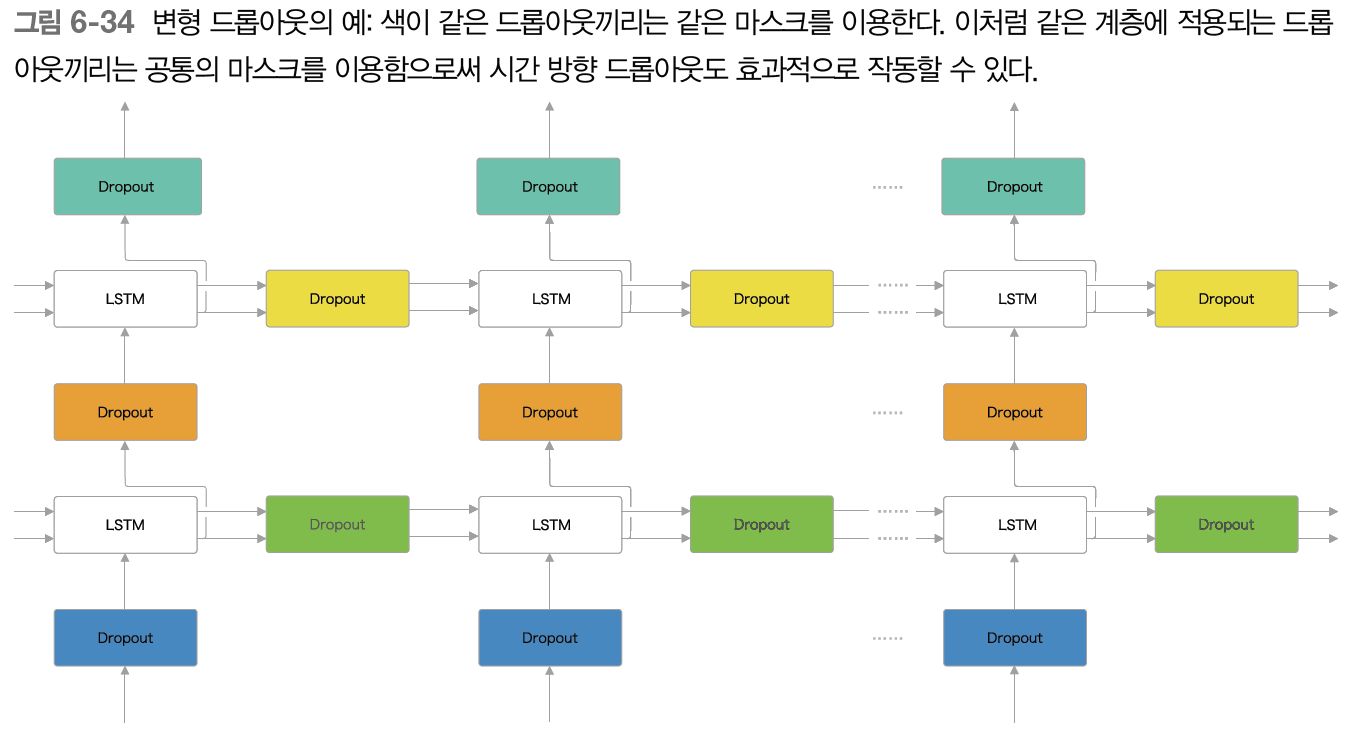
같은 계층의 드롭아웃 끼리 마스킹을 공유함으로써 마스크가 고정되고 그 결과 정보를 잃게 되는 방법도 고정되므로, 일반적인 드롭아웃 때와 달리 정보가 지수적으로 손실되는 사태를 피할 수 있다.
가중치 공유

두 계층이 가중치를 공유함으로써 학습하는 매개변수 수가 크게 줄어드는 동시에 정확도도 향상되는 기법이다. 예를 들어 어휘 수를 V, LSTM의 hidden state의 차원 수를 H라고 해보자. 그러면 Embedding 계층의 가중치는 VxH이며, Affine 계층의 가중치는 HxV가 된다. 따라서 하나의 가중치를 전치하여 다른 계층의 가중치로 사용할 수 있다.
'책 > 밑바닥부터 시작하는 딥러닝 2' 카테고리의 다른 글
| 7장 RNN을 사용한 문장 생성 (2) (0) | 2023.11.02 |
|---|---|
| 7장 RNN을 사용한 문장 생성 (1) (0) | 2023.11.01 |
| 6장 게이트가 추가된 RNN (1) (0) | 2023.10.27 |
| 5장 RNN (2) (0) | 2023.09.27 |
| 5장 RNN (1) (0) | 2023.09.26 |



