시계열 데이터 처리 계층 구현
RNN을 시계열 데이터 처리를 위해 TimeRNN 클래스를 구현한 것 처럼 Embedding, Affine, Softmax 계층도 Time 계층 구현이 필요하다. 그런 다음 이를 조합하면 RNNLM(RNN Language Model)을 구현할 수 있다.
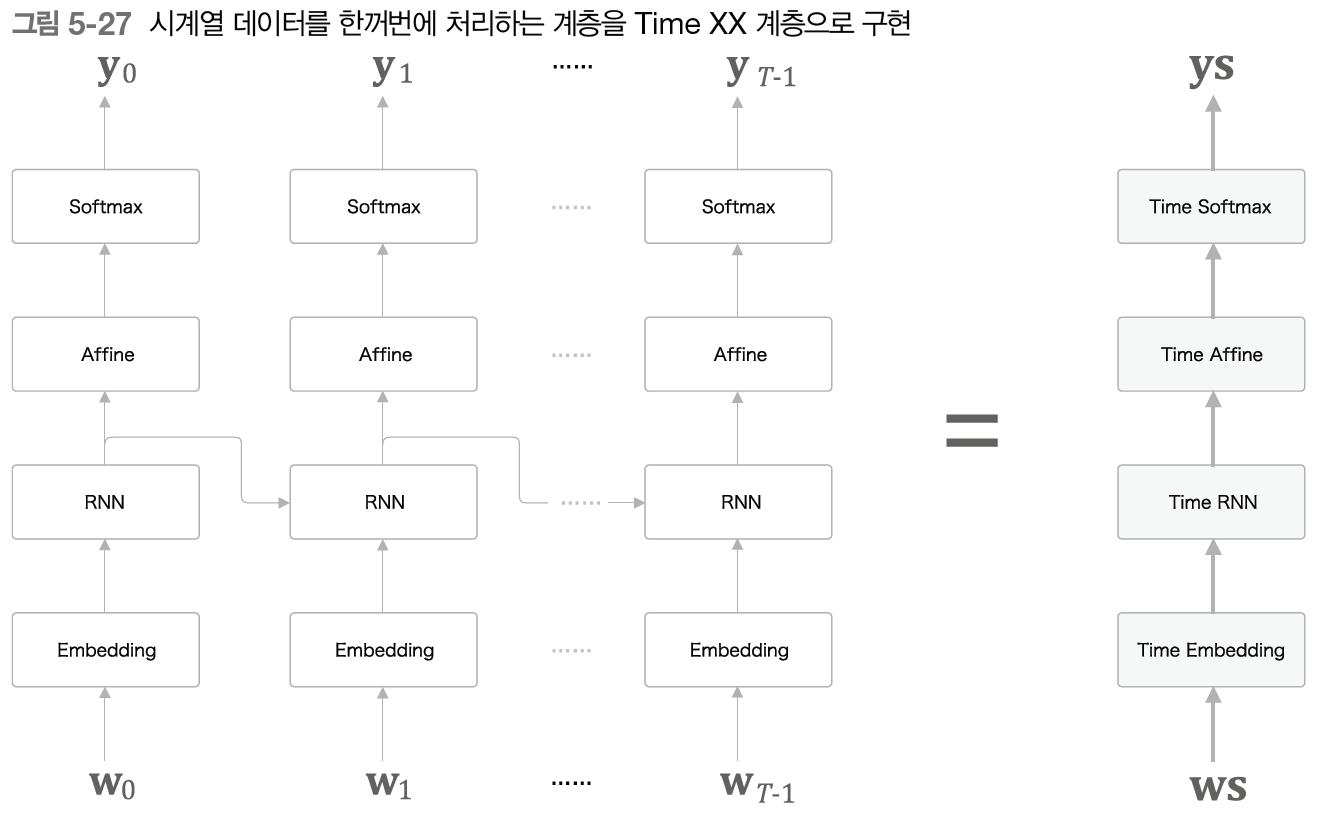
RNNLM의 처리는 다음과 같다.

현재 타임 스텝의 입력을 받고 그 다음 타임스텝의 단어를 예측한다. corpus로부터 데이터 입력과 정답을 만들어낼 때 다음과 같이 만들어야 한다.
xs = corpus[:-1] # 입력
ts = corpus[1:] # 정답Softmax with Loss 계층도 다음과 같이 Time 계층으로의 처리가 필요하다.

모든 타입 스텝의 손실함수를 더해서 평균한 것이 최종 손실이 된다. 수식으로는 다음과 같다.

언어 모델의 평가
perplexity 라는 지표가 있다. 간단하게는 확률의 역수이다. 예를 들어 정답이 say일 때 모델1이 say라고 예측한 확률이 0.8이면 perplexity는 그의 역수 1.25가 된다. 모델 2는 say라고 예측한 확률이 0.2라면 perplexity는 5가 된다. 따라서 perplexity 지표는 최소값이 1이고 그 값이 작을 수록 좋은 모델이라고 평가할 수 있다. 또 perplexity의 값을 단어의 후보의 개수라고 해석할 수도 있다.
위는 입력 데이터가 하나인 경우의 perplexity이고 미니배치의 경우엔 다음과 같이 계산한다.


식 5.12는 우리가 알고있는 크로스 엔트로피와 똑같다. 따라서 perplexity는 자연 상수에 최종손실함수만큼 제곱해준 값이다.
'책 > 밑바닥부터 시작하는 딥러닝 2' 카테고리의 다른 글
| 6장 게이트가 추가된 RNN (2) (0) | 2023.10.31 |
|---|---|
| 6장 게이트가 추가된 RNN (1) (0) | 2023.10.27 |
| 5장 RNN (1) (0) | 2023.09.26 |
| 4장 word2vec 속도 개선 (0) | 2023.09.26 |
| 3장 word2vec (0) | 2023.09.25 |



