word2vec 개선 (1)
은닉층의 뉴런이 100개인 CBOW 모델을 생각해보자
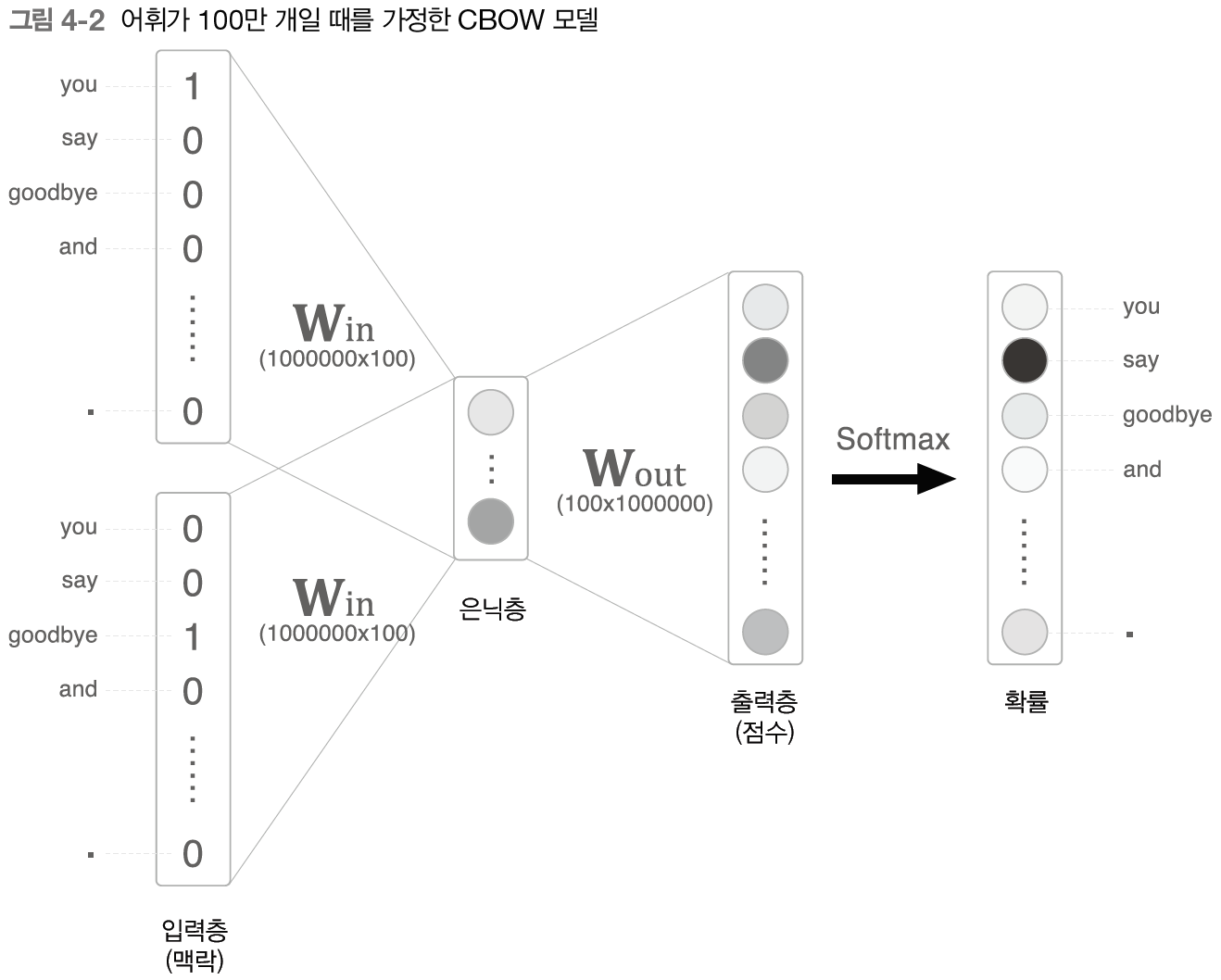
다음의 두 계산이 병목이 된다.
1. 입력층의 원핫 표현과 가중치 행렬 $W_{in}$의 곱 계산
뉴런의 크기가 100만개라면 원-핫 벡터는 상당한 메모리를 차지하게된다. 또 이 원핫 벡터와 가중치 행렬의 곱 계산에도 상당한 자원을 소모하게 된다. 이는 Embedding 계층을 도입하여 해결한다.
2. 은닉층의 가중치 행렬 $W_{out}$의 곱 및 Softmax 계층의 계산
마찬가지로 다루는 어휘가 많아짐에 따라 계산량이 증가한다. 이는 네거티브 샘플링이라는 새로운 손실 함수를 도입해 해결한다.
Embedding 계층

사실 이 계산은 단어 ID에 해당하는 행벡터를 추출하는 것뿐이다. 따라서 원핫 표현으로의 변환과 MatMul 계층의 행렬 곱은 필요가 없어지게 된다.
Embedding 계층 구현
class Embedding:
def __init__(self, W):
self.params = [W]
self.grads = [np.zeros_like(W)]
self.idx = None
def forward(self, idx):
W, = self.params
self.idx = idx
out = W[idx]
return outEmbedding 계층의 forward 메서드는 매우 쉽다. 가중치 행렬 W로 부터 인덱스에 해당하는 행벡터를 추출하기만 하면된다.
forward시 가중치의 특정 행 벡터를 다음 층으로 흘려보내기만 했기 때문에, 역전파시에도 앞 층의 gradient를 그대로 흘려주면 된다.

다만 앞 층으로부터 전해진 기울기 $dh$를 가중치 기울기 $dW$의 인덱스 행에 설정한다.
def backward(self, dout):
dW, = self.grads
dW[...] = 0
np.add.at(dW, self.idx, dout)
return Nonenp.add.at(A, idx, B)는 B를 A의 idx번째 행에 더해준다. idx가 array일 경우에도 가능하여 for 문을 사용하는 것보다 속도가 더 빠르다.
word2vec 개선 (2)
다중 분류에서 이진 분류로
you와 goodbye가 주어졌을 때 여러 어휘 중에서 타겟이 무엇인지를 추측하는 문제에서 타겟이 say인지 아닌지를 추측하는 문제로 바꾸는 아이디어이다.
CBOW 모델의 구조는 다음과 같이 바뀔 수 있다.

은닉층과 say에 해당하는 열벡터의 내적을 그림으로 표현하면 다음과 같다.

그런 다음 계산된 score에 시그모이드 함수를 이용해 확률로 변환하고 크로스 엔트로피 손실함수를 이용해 학습한다.
Embedding과 이진 분류가 적용된 신경망은 다음과 같다.
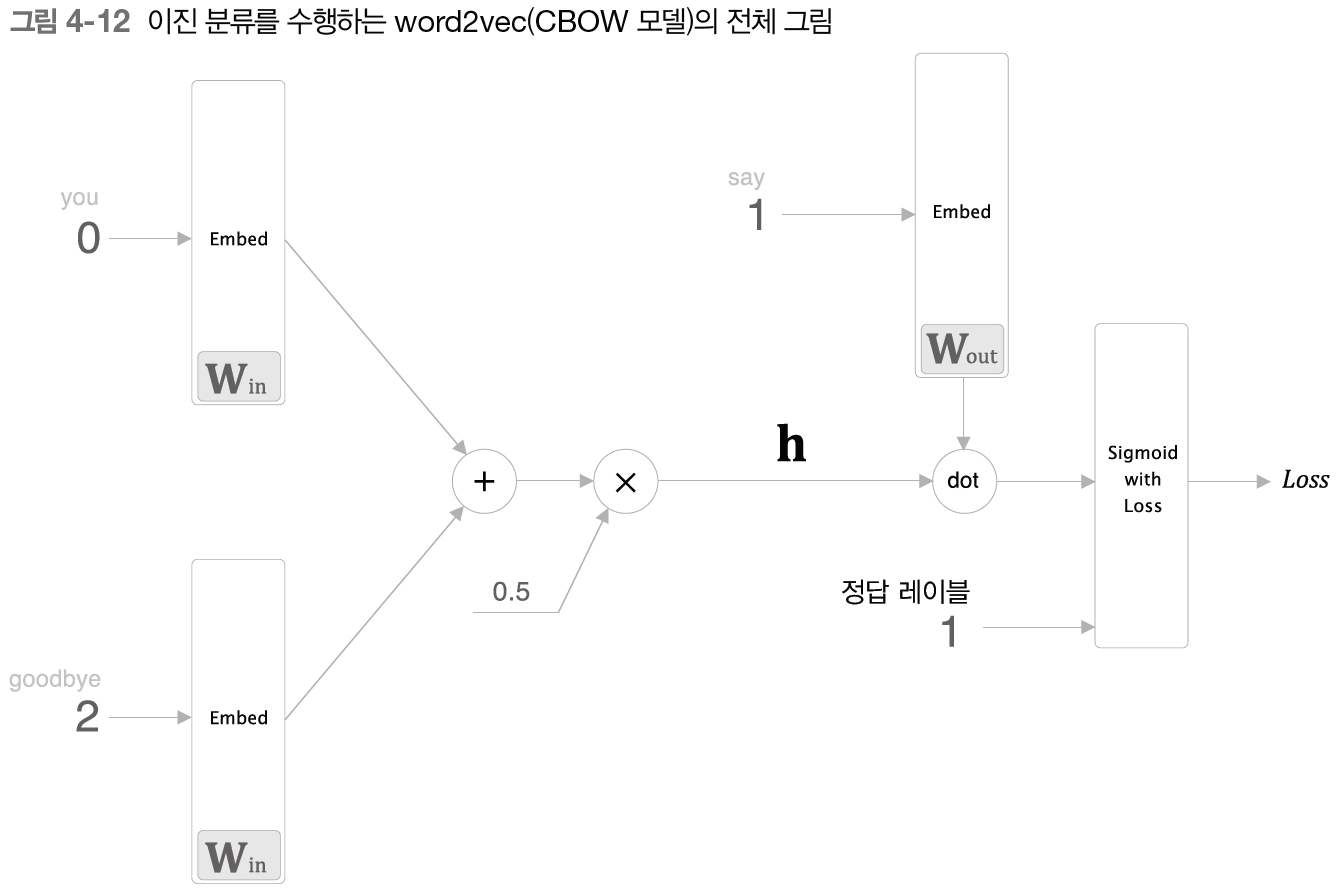
위 그림의 곱셈 노드 이후를 더 간소하게 표현하면 다음과 같다.

Embedding Dot 계층은 Embedding 계층과 내적을 합친 계층이다.
class EmbeddingDot:
def __init__(self, W):
self.embed = Embedding(W)
self.params = self.embed.params
self.grads = self.embed.grads
self.cache = None # forward 시의 계산 결과를 잠시 유지하기 위한 변수
def forward(self, h, idx):
target_W = self.embed.forward(idx)
out = np.sum(target_W * h, axis=1)
self.cache = (h, target_W)
return out
def backward(self, dout):
h, target_W = self.cache
dout = dout.reshape(dout.shape[0], 1)
dtarget_W = dout * h
self.embed.backward(dtarget_W)
dh = dout * target_W
return dh
네거티브 샘플링
지금까지는 정답 레이블(say)에 대해서만 생각했다. 좋은 신경망을 만들기 위해서는 오답 레이블에 대해서도 sigmoid 출력이 0이 나오도록 학습시켜야 한다. 그렇지만 모든 오답 레이블에 대해 학습하는 것은 어휘 수가 많은 경우 불가능 하기 때문에 오답 중 몇 개를 샘플링하여 사용한다.
정답 레이블에 대한 손실과, 샘플링된 오답 레이블에 대한 손실들을 모두 더해 최종 손실로 사용한다. 오답 레이블 2개를 샘플링 한 경우 은닉층 이후 계산 그래프는 다음과 같다.

오답 레이블을 샘플링 하는 방법은 말뭉치에서 단어의 출현 횟수를 구해 이를 확률 분포로 나타낸 뒤 이 확률분포에 기반하면 샘플링을 한다.
words = ['a', 'b', 'c', 'd']
p = [0.1, 0.2, 0.3, 0.4]
np.random.choice(words, p=p)네거티브 샘플링에서는 확률 분포에 0.75를 제곱하여 사용하라고 한다. 이는 낮은 확률 값을 조금 높이는 효과가 있다.
샘플링 담당하는 클래스 UnigramSampler 클래스의 구현은 다음과 같다.
class UnigramSampler:
def __init__(self, corpus, power, sample_size):
self.sample_size = sample_size
self.vocab_size = None
self.word_p = None
counts = collections.Counter()
for word_id in corpus:
counts[word_id] += 1
vocab_size = len(counts)
self.vocab_size = vocab_size
self.word_p = np.zeros(vocab_size)
for i in range(vocab_size):
self.word_p[i] = counts[i]
self.word_p = np.power(self.word_p, power)
self.word_p /= np.sum(self.word_p)
def get_negative_sample(self, target):
batch_size = target.shape[0]
if not GPU:
negative_sample = np.zeros((batch_size, self.sample_size), dtype=np.int32)
for i in range(batch_size):
p = self.word_p.copy()
target_idx = target[i]
p[target_idx] = 0
p /= p.sum()
negative_sample[i, :] = np.random.choice(self.vocab_size, size=self.sample_size, replace=False, p=p)
else:
# GPU(cupy)로 계산할 때는 속도를 우선한다.
# 부정적 예에 타깃이 포함될 수 있다.
negative_sample = np.random.choice(self.vocab_size, size=(batch_size, self.sample_size),
replace=True, p=self.word_p)
return negative_samplenp.random.choice() 메서드를 이용해 size에 지정된 수 만큼 샘플링을 한다. replace=False로 지정하면 중복이 없다.
이를 가지고 CBOW 모델 구현에 사용할 NegativeSamplingLoss 계층을 구현해보자
class NegativeSamplingLoss:
def __init__(self, W, corpus, power=0.75, sample_size=5):
self.sample_size = sample_size
self.sampler = UnigramSampler(corpus, power, sample_size)
self.loss_layers = [SigmoidWithLoss() for _ in range(sample_size + 1)]
self.embed_dot_layers = [EmbeddingDot(W) for _ in range(sample_size + 1)]
self.params, self.grads = [], []
for layer in self.embed_dot_layers:
self.params += layer.params
self.grads += layer.grads
def forward(self, h, target):
batch_size = target.shape[0]
negative_sample = self.sampler.get_negative_sample(target)
# positive sample
score = self.embed_dot_layers[0].forward(h, target)
correct_label = np.ones(batch_size, dtype=np.int32)
loss = self.loss_layers[0].forward(score, correct_label)
# negative sample
negative_label = np.zeros(batch_size, dtype=np.int32)
for i in range(self.sample_size):
negative_target = negative_sample[:, i]
score = self.embed_dot_layers[1 + i].forward(h, negative_target)
loss += self.loss_layers[1 + i].forward(score, negative_label)
return lossforward시 positive와 negative sample들에 대하여 loss를 구하고 이를 모두 더해준다.
def backward(self, dout=1):
dh = 0
for l0, l1 in zip(self.loss_layers, self.embed_dot_layers):
dscore = l0.backward(dout)
dh += l1.backward(dscore)
return dhbackward시에도 순전파에서 모두 더해준 것 처럼 sample마다 계산된 $dh$를 모두 더해서 리턴한다.
이를 이용한 CBOW 모델 클래스 구현은 다음과 같다.
class CBOW:
def __init__(self, vocab_size, hidden_size, window_size, corpus):
V, H = vocab_size, hidden_size
# 가중치 초기화
W_in = 0.01 * np.random.randn(V, H).astype('f')
W_out = 0.01 * np.random.randn(V, H).astype('f')
# 계층 생성
self.in_layers = []
for i in range(2 * window_size):
layer = Embedding(W_in) # Embedding 계층 사용
self.in_layers.append(layer)
self.ns_loss = NegativeSamplingLoss(W_out, corpus, power=0.75, sample_size=5)
# 모든 가중치와 기울기를 배열에 모은다.
layers = self.in_layers + [self.ns_loss]
self.params, self.grads = [], []
for layer in layers:
self.params += layer.params
self.grads += layer.grads
# 인스턴스 변수에 단어의 분산 표현을 저장한다.
self.word_vecs = W_in
def forward(self, contexts, target):
h = 0
for i, layer in enumerate(self.in_layers):
h += layer.forward(contexts[:, i])
h *= 1 / len(self.in_layers)
loss = self.ns_loss.forward(h, target)
return loss
def backward(self, dout=1):
dout = self.ns_loss.backward(dout)
dout *= 1 / len(self.in_layers)
for layer in self.in_layers:
layer.backward(dout)
return None초기화에서 계층을 생성할 때 window_size의 2배로 해주는 이유는 타겟 단어로 부터 양 옆의 맥락을 사용하기 때문이다.
CBOW 모델 평가
앞에서 구현한 CBOW 모델을 ptb 데이터셋에 학습하였다. 2장에서 구현한 most_similar() 메서드를 이용해, 단 어 몇개에 대해 거리가 가장 가까운 단어들을 뽑아보자.
pkl_file = 'cbow_params.pkl'
# pkl_file = 'skipgram_params.pkl'
with open(pkl_file, 'rb') as f:
params = pickle.load(f)
word_vecs = params['word_vecs']
word_to_id = params['word_to_id']
id_to_word = params['id_to_word']
# 가장 비슷한(most similar) 단어 뽑기
querys = ['you', 'year', 'car', 'toyota']
for query in querys:
most_similar(query, word_to_id, id_to_word, word_vecs, top=5)결과는 다음과 같다.
[query] you
we: 0.6103515625
someone: 0.59130859375
i: 0.55419921875
something: 0.48974609375
anyone: 0.47314453125
[query] year
month: 0.71875
week: 0.65234375
spring: 0.62744140625
summer: 0.6259765625
decade: 0.603515625
[query] car
luxury: 0.497314453125
arabia: 0.47802734375
auto: 0.47119140625
disk-drive: 0.450927734375
travel: 0.4091796875
[query] toyota
ford: 0.55078125
instrumentation: 0.509765625
mazda: 0.49365234375
bethlehem: 0.47509765625
nissan: 0.474853515625이번에는 유추 문제를 풀어보자. word2vec으로 얻은 단어의 분산 표현은 비슷한 단어를 가까이 모을 뿐 아니라, 더 복잡한 패턴도 파악할 수 있다. 대표적인 예가 다음과 같은 문제이다.

벡터 공간에서 vec_?을 구하기 위해서는 vec_king + vec_woman - vec_man을 계산하면 된다. 이 로직을 구현한 메서드 analogy()는 다음과 같다.
def analogy(a, b, c, word_to_id, id_to_word, word_matrix, top=5, answer=None):
for word in (a, b, c):
if word not in word_to_id:
print('%s(을)를 찾을 수 없습니다.' % word)
return
print('\n[analogy] ' + a + ':' + b + ' = ' + c + ':?')
a_vec, b_vec, c_vec = word_matrix[word_to_id[a]], word_matrix[word_to_id[b]], word_matrix[word_to_id[c]]
query_vec = b_vec - a_vec + c_vec
query_vec = normalize(query_vec)
similarity = np.dot(word_matrix, query_vec)
if answer is not None:
print("==>" + answer + ":" + str(np.dot(word_matrix[word_to_id[answer]], query_vec)))
count = 0
for i in (-1 * similarity).argsort():
if np.isnan(similarity[i]):
continue
if id_to_word[i] in (a, b, c):
continue
print(' {0}: {1}'.format(id_to_word[i], similarity[i]))
count += 1
if count >= top:
returnquery_vec을 계산한 뒤 이를 normalize해주는 부분이 있는데, normalize는 element 값을 정규화하고 word_matrix와 내적 계산이 가능하도록 reshape해준다. 예를 들어 word_matrix의 shape이 (100, 3)이라고 하면 100개의 단어가 있고 이들을 3차원 벡터로 표현한 것이다. query_vec은 당연히 (1, 3)일테고 이를 (3, 1)로 reshape 해주어야 word_matrix와 내적하여 (100, 1)의 벡터를 얻을 수 있다. 이것이 similarity이고 각 행에는 query_vec과의 유사도 점수가 담겨 있다.
유추를 해보면 다음과 같다.
# 유추(analogy) 작업
print('-'*50)
analogy('king', 'man', 'queen', word_to_id, id_to_word, word_vecs)
analogy('take', 'took', 'go', word_to_id, id_to_word, word_vecs)
analogy('car', 'cars', 'child', word_to_id, id_to_word, word_vecs)
analogy('good', 'better', 'bad', word_to_id, id_to_word, word_vecs)
[analogy] king:man = queen:?
woman: 5.16015625
veto: 4.9296875
ounce: 4.69140625
earthquake: 4.6328125
successor: 4.609375
[analogy] take:took = go:?
went: 4.55078125
points: 4.25
began: 4.09375
comes: 3.98046875
oct.: 3.90625
[analogy] car:cars = child:?
children: 5.21875
average: 4.7265625
yield: 4.20703125
cattle: 4.1875
priced: 4.1796875
[analogy] good:better = bad:?
more: 6.6484375
less: 6.0625
rather: 5.21875
slower: 4.734375
greater: 4.671875두세 번째 문제에서 과거형, 단복수에 대한 패턴을 파악하고 있음 알고 있지만 마지막 문제에서는 worse라고 대답하지는 않았다. 그렇지만 more, less 등의 답변을 하는 것으로 보아 비교급이라는 특징은 단어의 분산 표현에 인코딩되어 있음을 알 수 있다.
'책 > 밑바닥부터 시작하는 딥러닝 2' 카테고리의 다른 글
| 6장 게이트가 추가된 RNN (1) (0) | 2023.10.27 |
|---|---|
| 5장 RNN (2) (0) | 2023.09.27 |
| 5장 RNN (1) (0) | 2023.09.26 |
| 3장 word2vec (0) | 2023.09.25 |
| 2장 자연어와 단어의 분산 표현 (0) | 2023.09.24 |



