Exhaustive Search 전역 탐색
가능한 경우를 모두 탐색하는 것이다. 변수가 $n$개가 있다면 변수의 조합 개수는 $2^n - 1$이다. 당연히 변수의 개수가 많을 수록 사용할 수 없는 방법론이다.

위 그래프를 보면 1초에 10000개의 모델을 평가할 수 있는 계산 속도를 가지고 있어도 변수의 개수가 40개만 되더라도 1년이 걸린다.
변수를 평가할 때는 Akaike Information Criteria(AIC), Bayesian Information Criteria(BIC), Adjusted R-squared 등을 사용한다.
Adjusted R-squared의 수식은 다음과 같다.
$1 - {{(1-R^2)\cdot(n-1)} \over {n-k-1}}$
$R^2$: 일반적인 R-squared
$n$: 샘플 수
$k$: 모델에 포함된 독립 변수의 수
나머지 두 수식은 다음과 같다.

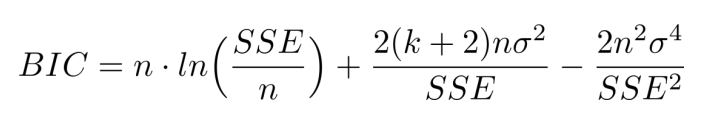
AIC 정도만 알아도 충분하다고 한다.
Forward Selection 전진 선택
- 변수가 없는 상태에서 가장 중요할 것으로 생각되는 변수가 순차적으로 적용된다.
- 한 번 선택된 변수는 다시 제거되지 않는다.
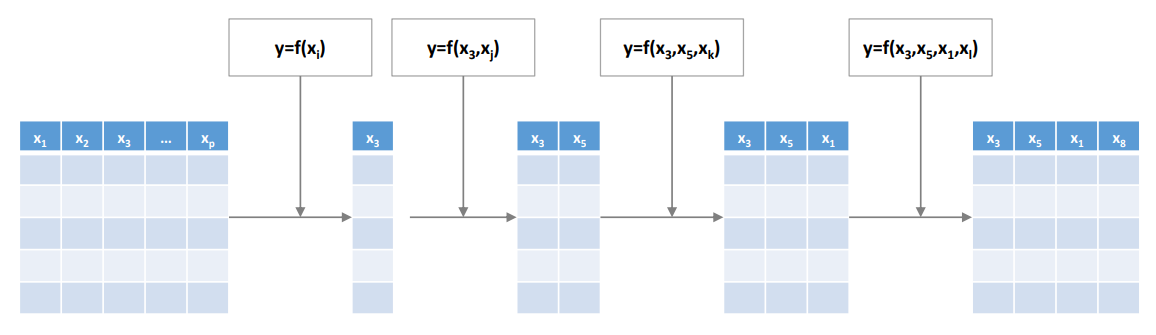
$x_1 ... x_p$ 변수가 있을 때 처음에는 하나씩 변수를 넣어보면서 Adjusted R-squared을 계산한다. 위 그림에서는 이 경우에 $x_3$이 평가 점수가 가장 좋아서 채택되었다. 그런 다음 $x_3$은 고정한 상태로 다시 나머지 변수들을 하나씩 넣어보면서 평가한다.
이런식으로 순차적으로 변수를 추가하다가 모델의 성능이 더 이상 유의미하게 증가하지 않을 때 종료된다.
Backward Elimination 후방 소거
Forward Selection과는 정반대로 처음에는 모든 변수를 포함한 모델로 출발하여, 변수를 순차적으로 하나씩 제거한다. 어떤 변수를 제거하였을 때 성능의 차이가 없거나 성능이 더 증가하는 경우에 해당 변수를 제거하는 것이다.
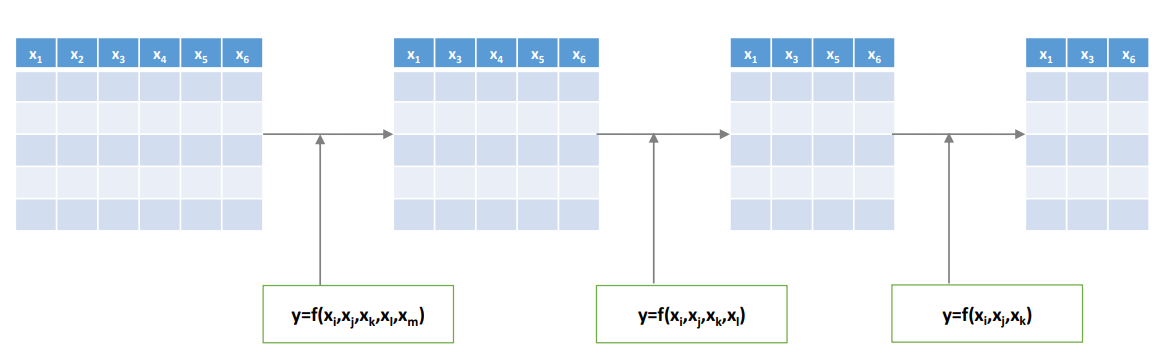
현재 조합에서 어떤 변수를 빼더라도 성능의 저하가 급격하게 발생한다면 종료된다.
Stepwise Selection
- 전진 선택과 후방 소거를 번갈아가면서 수행한다.
- 따라서 시간이 더 오래 걸리지만 최적의 변수 조합을 찾을 가능성이 증가한다.
- 한 번 선택되거나 제거된 변수들이 다시 선택이나 제거의 후보군이 될 수 있다.
예를 들어 $x_3, x_5$에서 전진 선택을 사용해 $x_1, x_3, x_5$의 조합을 찾았다. 여기서 다시 후방 소거를 진행한다. 그러면 이전에는 보지 못헀던 $x_1, x_3$ 조합의 성능을 확인할 수 있다. 종료 조건은 전진 선택과 후방 선택의 종료 조건과 같다.
아래 코드는 OLS를 사용하여 선형 회귀 모델을 적합하고 ANOVA를 사용해 F 통계량을 추출하여 stepwise selection을 수행하는 예시이다.
import pandas as pd
import numpy as np
import statsmodels.api as sm
def forward_backward_selection(data, target_col, significance_level=0.05):
remaining_vars = set(data.columns)
remaining_vars.remove(target_col)
selected_vars = []
while True:
best_var = None
best_model = None
best_p_value = np.inf
for var in remaining_vars:
X = data[selected_vars + [var]]
X = sm.add_constant(X)
y = data[target_col]
model = sm.OLS(y, X).fit()
p_value = model.pvalues[var]
if p_value < best_p_value:
best_p_value = p_value
best_var = var
best_model = model
if best_p_value < significance_level:
selected_vars.append(best_var)
remaining_vars.remove(best_var)
if not remaining_vars:
break
else:
break
while True:
X = data[selected_vars]
X = sm.add_constant(X)
y = data[target_col]
model = sm.OLS(y, X).fit()
p_values = model.pvalues.iloc[1:] # exclude constant term
if all(p > significance_level for p in p_values):
break
worst_var = p_values.idxmax()
selected_vars.remove(worst_var)
return selected_vars
Genetic Algorithm
Forward, backward, stepwise를 local search라고 부른다. Local search는 효율적인 탐색 방법이지만 탐색 영역이 매우 제한적이어서 최적의 조합을 찾을 확률이 낮아질 수 있다.
Genetic Algorithm은 local search에서 약간의 계산 시간을 더 투자하여 local search를 향상시키는 것이 목적이다. 프로세스는 6단계로 이루어지고, 2단계와 5단계 사이에는 피드백 루프가 있다.
Step 1: Initialize Chromosomes

유전 알고리즘이라 유전 관련 용어가 등장하는데 Gene은 변수를 의미한다. Chromosome은 binary encoding으로 gene의 사용 여부를 나타낸 것이다. 1이면 해당 gene을 사용, 0이면 사용하지 않는다.
1단계에서는 파라미터들을 초기화한다.
- chromosome의 개수 - 일반적으로 50~100개를 사용하며 전체 chromosome을 population이라 부른다.
- fitness function - chromosome을 평가하기 위한 함수
- crossover mechanism
- rate of mutation
- 종료 조건
Step 2: 모델 학습
Step 3: Fitness Evaluation
사전에 정의한 fitness function으로 chromosome들을 평가한다.
- fitness value가 동일하다면 더 적은 변수를 사용하는 chromosome이 선호된다.
- 사용 변수의 개수가 같다면 더 높은 예측 성능을 보이는 chromosome이 선호된다.
예를 들어 multiple linear regression을 수행한다면, fitness function으로 Adjusted R2, AIC, BIC를 사용할 수 있다.
Step 4: Selection
- Deterministic selection: 상위 N%의 chromosome만 선택하는 방식
- Probabilistic selection: fitness value에 따라 chromosome에 가중치를 주어 확률적으로 선택하는 방식
Step 5: Crossover & Mutation
Crossover
- 2개의 부모 chromosome으로부터 2개의 자식 chromosome을 생성하는 방식이다.
- crossover point는 gene의 총 개수가 n개라면 1 ~ n 까지 다양하게 지정할 수 있다.
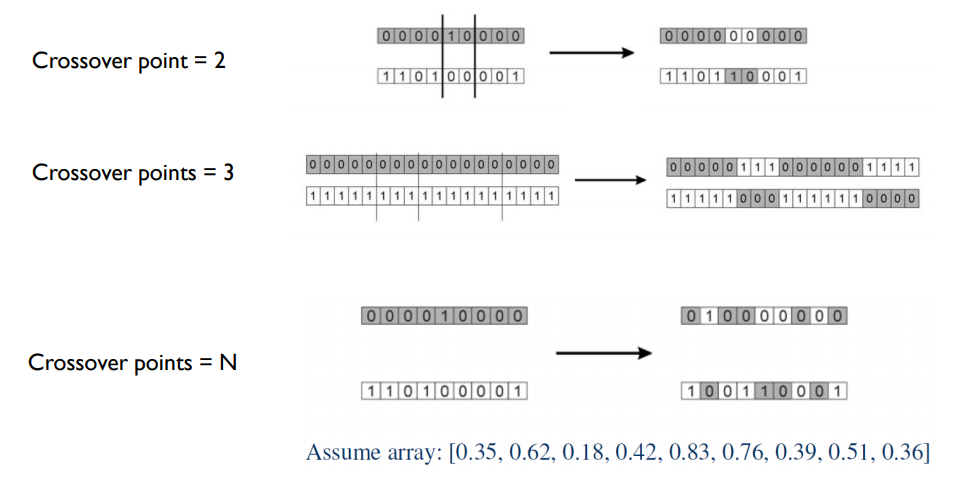
point 값에 따라서 gene이 서로 바뀌는 구간을 정한다. 그리고 교차 방식으로 encoding 값을 서로 바꾼다. point가 2일 때는 처음에는 안바꾸다가 미리 지정한 point가 나오면 서로 바꾼다. 그 다음 point는 안바꾼다. point가 3일 때도 교차하면서 서로의 값을 바꾼다.
point가 n개 일때는 길이가 n인 난수를 생성한다. 그리고 난수 값이 0.5 이상인 부분만 서로를 교체한다. 따라서 point를 n개로 지정하는 방식이 자유도가 높다.
Mutation
위의 방법으로 생성된 자식 chromosome의 gene에 1% 미만의 확률로 변이를 주는 것이다. 이는 local minimum을 탈출하는데 도움이 된다.

6단계에서는 2 ~ 5단계를 계속 반복하면서 종료 조건을 만족하였을 때 가장 높은 fitness value를 가지는 chromosome을 최종적으로 선택한다. 일반적으로 초기 세대에서는 fitness value가 상당히 증가하다가 일정 값으로 수렴하게 된다.
'Machine Learning > Business Analytics 1' 카테고리의 다른 글
| Dimensionality Reduction - Overview (0) | 2024.04.04 |
|---|---|
| Classification Performance Evaluation (0) | 2023.12.20 |
| Logistic Regression : Interpretation (0) | 2023.12.20 |
| Logistic Regression : Learning (0) | 2023.12.19 |
| Logistic Regression : Formulation (0) | 2023.12.19 |



