계산 그래프
계산 그래프는 계산 과정을 그래프로 나타낸 것이고, 노드와 에지로 표현된다.
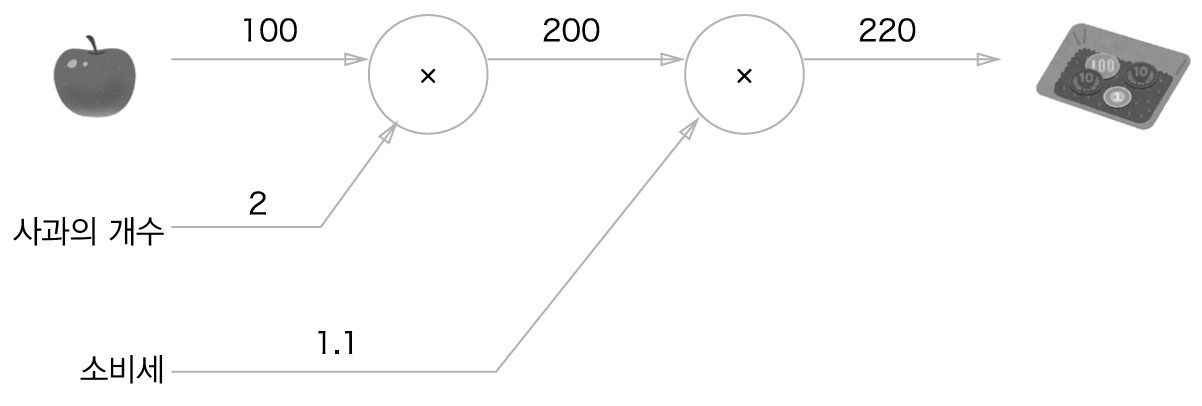
이렇게 생겼다.

역전파는 반대 방향의 굵은 화살표로 표현한다. 역전파의 엣지 값이 전달되는 미분 값이다. 근데 솔직히 이렇게 숫자로 되어있는 것으로 보면 더 헷갈린다. 그냥 수식으로 보는게 낫다
계산 그래프의 역전파

노드를 기준으로 $y = f(x)$ 라는 수식을 정의하고 ${\partial y}/{\partial x}$ 을 구한뒤 상류에서 흘러들어온 미분값 E에 ${\partial y}/{\partial x}$ 을 곱해서 하류에 전달한다. 이 규칙만 지키면 된다.
덧셈 노드의 역전파
$z = x + y$라는 식이 있고, z의 x에 대한 편미분, y에 대한 편미분은 다음과 같다.

이를 계산 그래프로 표현하면 다음과 같다.
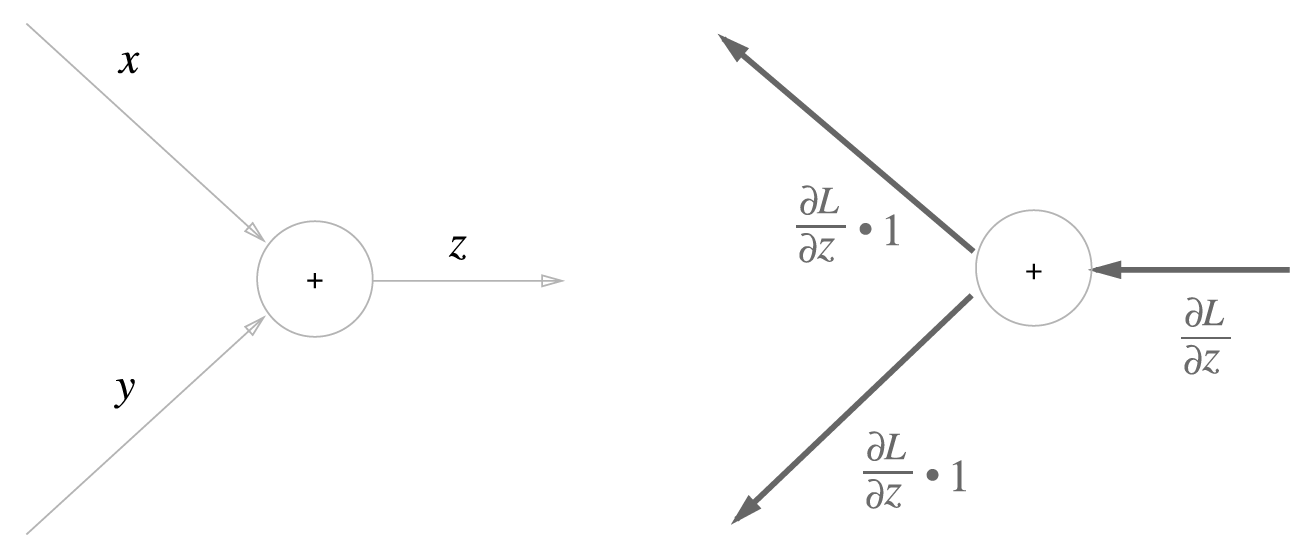
x쪽은 ${\partial z}/{\partial x}$, y쪽은 ${\partial z}/{\partial y}$가 곱해져 있는것이고 이 값이 1인 것이다. 어쨋든 덧셈노드는 상류에서 흘러들어온 미분값을 하류에 그대로 전달한다.
덧셈 노드를 코드로 구현해보자.
class AddLayer:
def __init__(self):
pass
def forward(self, x, y):
out = x + y
return out
def backward(self, dout):
dx = dout * 1
dy = dout * 1
return dx, dy덧셈 노드의 초기화에서는 아무것도 안해도 된다.
dout이 상류에서 흘러들어온 미분값이다. backward를 수행할 때 꼭 입력해줘야 한다.
곱셈 노드의 역전파
$z = xy$라는 식을 생각해보자. 마찬가지로 편미분은 다음과 같다.

이를 계산 그래프로 표현하면 다음과 같다.

x, y를 서로 바꿔서 곱해준다.
코드로 구현해보자
class MulLayer:
def __init__(self):
self.x = None
self.y = None
def forward(self, x, y):
self.x = x
self.y = y
out = x * y
return out
def backward(self, dout):
dx = dout * self.y
dy = dout * self.x
return dx, dybackward를 수행하기 전에는 꼭 forward를 수행해야 한다.
활성화 함수 계층 구현하기
신경망을 구성하는 층 각각을 클래스로 구현
ReLU

x에 대한 y의 미분은 다음과 같다.

이를 계산 그래프로 표현하면 다음과 같다

코드로 구현해보자
class Relu:
def __init__(self):
self.mask = None # True/False로 구성된 넘파이 배열
def forward(self, x):
self.mask = (x <= 0)
out = x.copy()
out[self.mask] = 0
return out
def backward(self, dout):
dout[self.mask] = 0
dx = dout
return dx- mask 라는 인스턴스 변수를 사용해 0보다 작거나 같은 값들을 처리한다.
Sigmoid

이를 계산 그래프로 표현하면 다음과 같다.

이의 역전파를 알아보자
1단계
'/' 노드는 $y = 1/x$ 를 의미한다. 여기서 y는 순전파시 출력, x는 순전파시 입력이다.
이를 미분하면 다음과 같다.

즉, 상류에서 흘러들어온 값에 순전파의 출력을 제곱한 후 마이너스를 붙인 값을 곱해서 하류로 전달한다.

2단계
앞에서 덧셈노드는 미분 값을 그대로 전달한다고 했다.

3단계
'exp' 노드는 $y = e^x$ 연산을 수행하며, 그 미분은 그대로 $e^x$ 이다.

4단계
곱셈 노드는 순전파 떄의 값을 서로 바꿔 곱해준다.

이 중간 과정을 모두 묶어 하나의 sigmoid 노드로 대체할 수 있다.

해석적인 미분값과 chain-rule을 사용해 계산량을 획기적으로 줄일 수 있다.
마지막으로 이를 정리해서 쓸 수 있다.

코드로 구현해보자
class Sigmoid:
def __init__(self):
self.out = None
def forward(self, x):
out = sigmoid(x)
self.out = out
return out
def backward(self, dout):
dx = dout * (1.0 - self.out) * self.out
return dxforward 출력을 인스턴스 변수 out에 보관했다가, 역전파 계산 때 사용한다.
Affine 계층
신경망의 순전파 때 수행하는 행렬의 곱을 기하학에서 affine transform이라고 한다. activiation이 없는 Dense layer로 보면된다.
이를 계산 그래프로 표현하면 다음과 같다.

역전파를 포함한 계산 그래프는 다음과 같다.

행렬의 미적분은 선형대수학 개념인데 대학에서 선형대수학을 배워본적이 없어서 잘 모르지만 직접 손으로 유도해보니 다음과 같은 결과가 나왔다.

https://en.wikipedia.org/wiki/Matrix_calculus
Matrix calculus - Wikipedia
From Wikipedia, the free encyclopedia Specialized notation for multivariable calculus In mathematics, matrix calculus is a specialized notation for doing multivariable calculus, especially over spaces of matrices. It collects the various partial derivative
en.wikipedia.org
여기를 참고하면 그리 어렵지 않게 유도가 가능하다. 그리고 어디에(앞인지, 뒤인지) dot product를 행해야 할지는 행렬의 대응하는 차원의 원소 수를 보고 판단하면 될 것 같다.
위는 입력 데이터 하나에 대한 것만 고려한 것이고 배치용 Affine 계층의 계산 그래프는 다음과 같다.

앞에 배치 차원수 N이 추가된 것 말고는 계산은 동일하다.
이를 클래스로 구현해보자
class Affine:
def __init__(self, W, b):
self.W = W
self.b = b
self.x = None
self.original_x_shape = None
self.dW = None
self.db = None
def forward(self, x):
self.original_x_shape = x.shape
x = x.reshape(x.shape[0], -1)
self.x = x
out = np.dot(self.x, self.W) + self.b
return out
def backward(self, dout):
dx = np.dot(dout, self.W.T)
self.dW = np.dot(self.x.T, dout)
self.db = np.sum(dout, axis=0)
dx = dx.reshape(*self.original_x_shape)
return dx- forward 부분에서 x를 reshape 해주는 이유는 x가 4차원일 경우도 고려한 것이다.
- backward에서 dx를 x의 원래 shape으로 reshape 해주는 이유는 ${\partial L}/{\partial X}$의 shape이 $X$의 shape과 같기 때문이다.
- 덧셈 노드는 미분값을 그대로 전달하는데 편향 벡터는 dout을 그대로 받는다. 그러나 shape이 맞지 않아 첫 번째 차원을 기준으로 sum 해주어 shape을 맞춰준다.
'책 > 밑바닥부터 시작하는 딥러닝' 카테고리의 다른 글
| 6장 학습 관련 기술들 (1) (0) | 2023.09.20 |
|---|---|
| 5장 오차역전파법 (2) (0) | 2023.09.19 |
| 4장 신경망 학습 (2) (0) | 2023.09.14 |
| 4장 신경망 학습 (1) (0) | 2023.09.13 |
| 3장 신경망 (0) | 2023.09.13 |


