- 서로 다른 모델들은 다른 클래스 바운더리나 fitted functions을 제공한다.
- 어떠한 single best model도 다른 알고리즘들에 비해서 우월하다는 결론을 내릴 수 없기 때문에 다양한 모델들이 기저가 된다.
이론 배경
데이터가 additive error를 가진 모델에서 나온다고 가정해보자

- F∗(x)는 우리가 학습하려고 하는 target function이다.
- error들은 각각 독립적이고 동일한 분포에서 발생되었다.

- F∗(x)을 추정하기 위해 서로 다른 데이터셋들로 부터 만든 함수를 ˆFN(x)이라 한다.
- ˆFN(x)들을 average한 것이 ˉF(x)라 한다.
특정한 데이터 포인트에서 MSE 에러가 어떻게 발생하는지 알아보자

- 2가지만 기억하면 이해하기 쉽다. 에러는 정규 분포에서 나왔다고 가정하기 때문에 에러의 평균은 0이다. 따라서 2E[A⋅B]=0이다.
- 에러의 기대값의 제곱은 에러의 분산이다.

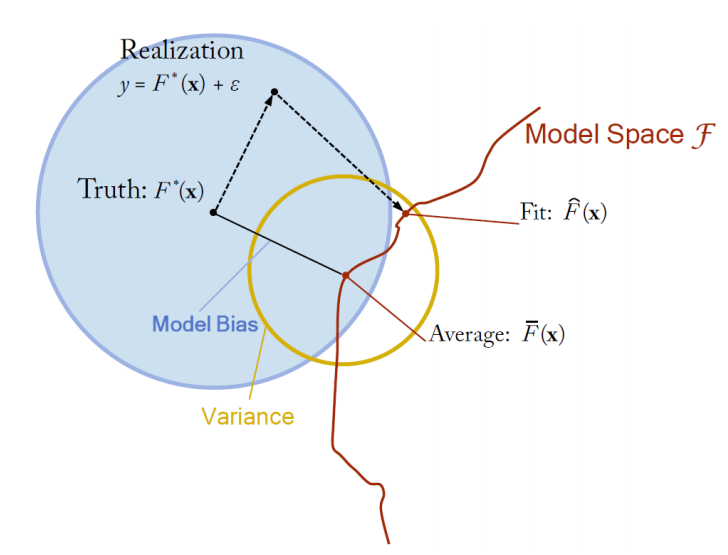
- 파란색에 해당하는 부분은 noise를 달리하며 모델링을 했을 때 모델들의 평균과 target funtion이 얼마나 차이가 나는지 즉, 편향을 의미한다.
- 빨간색은 noise를 달리하며 모델링을 했을 때 개별 모델들이 평균과 얼마나 큰 차이를 보이는가 즉, 분산을 의미한다.
정리해보자면
Bias2 : 평균 추정이 실제값과 얼마나 다른지
- low bias : 평균적으로 데이터셋으로 부터 정확하기 타겟 함수를 추정
- high bias : 좋지 않다
Variance : 개별적인 추정들이 그들의 평균으로부터 얼마나 퍼져있는지
- low : 다른 데이터셋으로 부터 추정 함수가 별로 바뀌지 않는다.
- high : 좋지 않다.
에러의 분산은 제거할 수 없는 에러
그림으로 이해해보자면 다음과 같다.
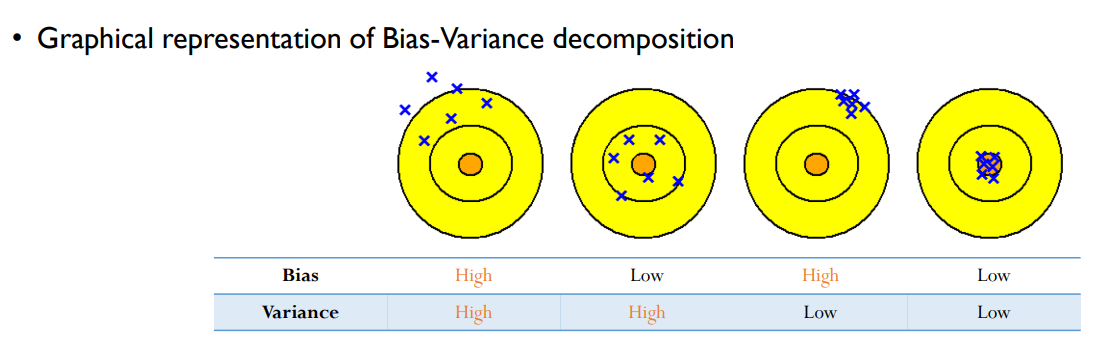
- 복잡도가 낮은 모델 : high bias & low variance
- 복잡도가 높은 모델 : low bias & high variance
- 2번에서 4번으로 갈 때는 bagging 기법을 사용하고, 3번에서 4번으로 갈 때는 boosting 기법을 사용한다.
Ensemble의 목적
목표 : 다수의 learner를 구성함으로써 에러를 줄인다.
- 분산을 줄이자 : bagging
- 편향을 줄이자 : boosting
ensemble 구성의 2가지 주요 questions
- 어떻게 하면 개별적인 모델의 다양성을 확보할 것인가? -> 핵심
- 개별 모델들의 출력을 어떻게 결합할 것인가?
Ensemble의 다양성
동일한 모델들을 결합하는 것으로 부터 Ensemble이 얻는 것은 없다.
- base learner들은 서로 적절하게 달라야 한다.
- 다양성을 확보하면서도 개별적으로 좋은 성능을 보여야 한다.
다양성에는 다음과 같이 2가지가 있다.

- Implicit : 데이터셋을 다르게 제공
- explicit : 명시적으로 어떠한 측정 지표를 주어서 이전 모델과 다른 모델이 만들어지도록 유도
Ensemble이 왜 좋은가?
실제 함수, 추정기, 에러가 주어졌을 때 다음과 같이 수식으로 표현할 수 있다.
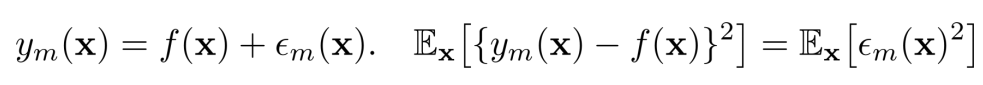
M개의 개별적인 모델들로 만들어진 평균 에러 vs 앙상블의 기대 에러
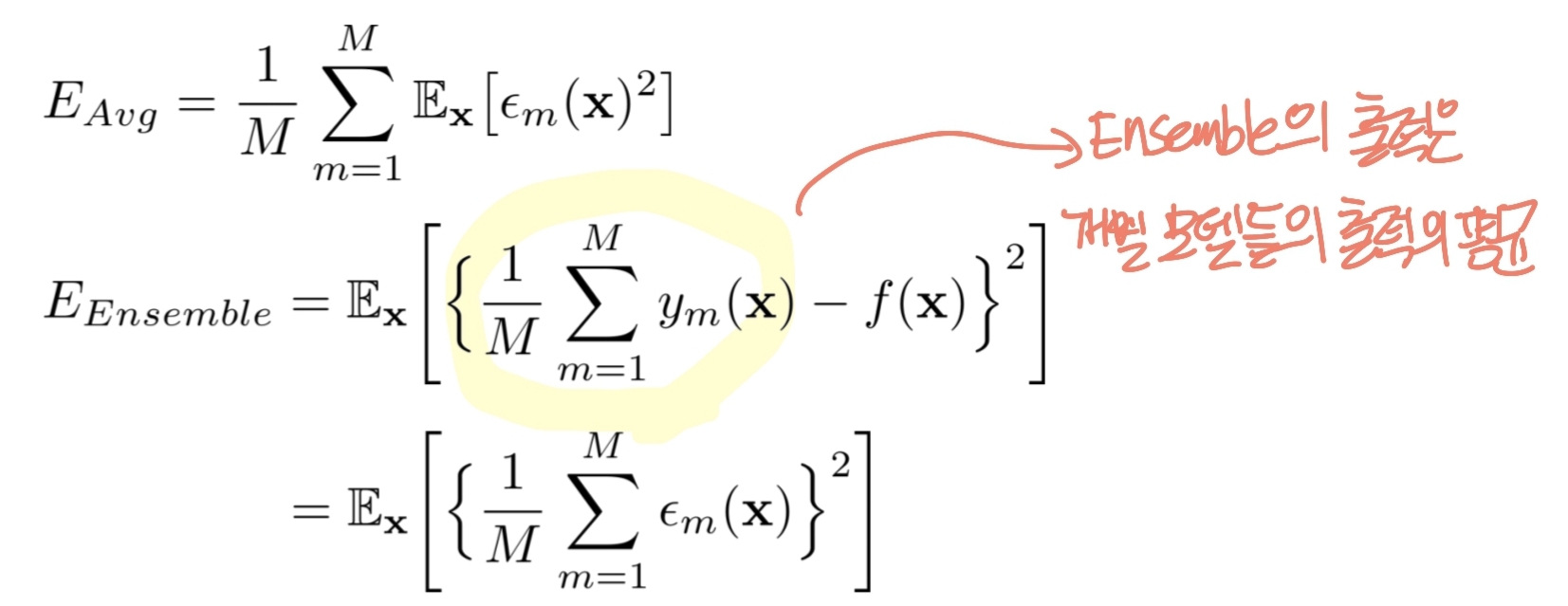
이를 정리하면 다음과 같다.
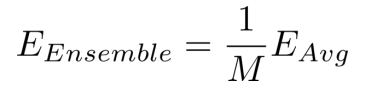
그렇지만 위와 같은 수식은 현실적으로는 불가능 하다.
현실에서는 코시-슈바르츠 공식에 따라 다음과 같이 유도하는 것이 가능하다.
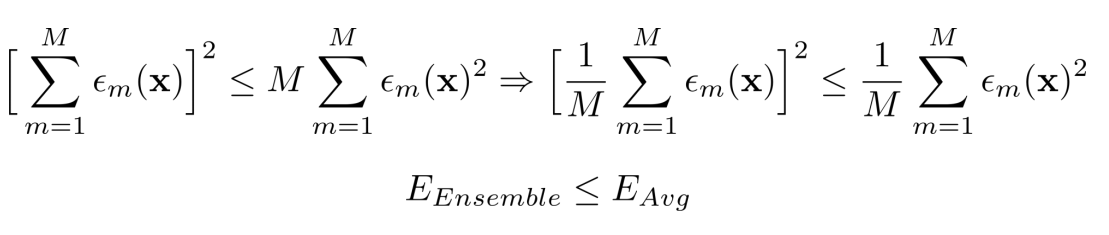
모든 경우에서 Ensemble이 single 모델보다 좋은 것은 절대 아니지만 대부분의 경우에서 Ensemble이 더 좋다.
'Machine Learning > Business Analytics 2' 카테고리의 다른 글
| 4-7 : Ensemble Learning - XGBoost (0) | 2023.12.29 |
|---|---|
| 4-6 : Ensemble Learning - Gradient Boosting Machine (GBM) (0) | 2023.12.28 |
| 4-5 : Ensemble Learning - Adaptive Boosting (AdaBoost) (0) | 2023.12.18 |
| 4-4 : Ensemble Learning - Random Forest (0) | 2023.12.18 |
| 4-3 : Ensemble Learning - Bagging (0) | 2023.12.11 |



