Gradient Boosting은 Gradient Descent 알고리즘과 Boosting이 결합된 알고리즘이다. Adaboost의 경우 forward stage-wise 방법으로 additive model을 만들고, 각 단계에서는 이전의 weak learner를 보완하는 새로운 weak learner를 제시하는 형태로 학습이 진행되었고, 잘 학습되지 않았던 shortcomings에 대해서는 다음 데이터셋에서 shortcomings의 weight을 조정하는 방법으로 모델을 학습시켰다.
반면에 Gradient Boosting에서는 shortcomings들이 gradient에 반영이 된다.
손실함수의 복잡도 측면에서 regression이 GBM 알고리즘을 직관적으로 이해하기 쉽기 때문에 regression으로 GBM을 이해해보자.
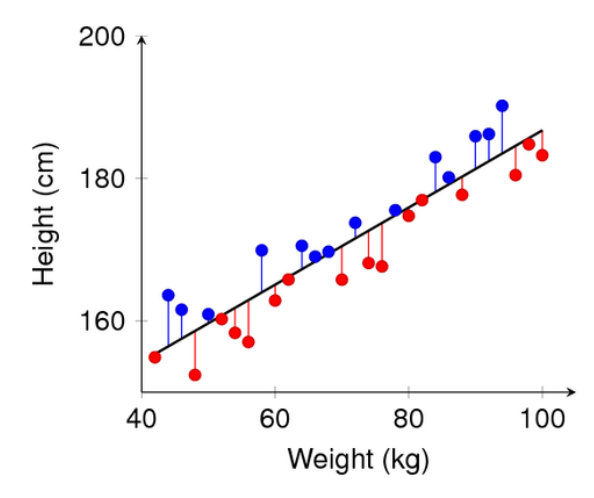
- 위와 같은 회귀 모형이 있을 때 모델의 회귀식(검정색 직선)을 $\hat y = f_1(x)$와 같이 표현할 수 있다.
- 이 때 $y-f_1(x)$을 residual(잔차)라고 한다. Adaboost에서는 각 단계마다 weight을 조정했던 반면 GBM에서는 데이터는 그대로 두고 (새로 샘플링을 하지 않고) 타겟값을 변경한다.
- 즉 $y-f_1(x) = f_2(x)$이 성립하는 새로운 타겟값으로 $f_2(x)$에 대해서 학습한다.
- 그리고 이 과정을 여러번 반복하여 수행한다.
이를 그림으로 표현하면 다음과 같다.

처음에는 original dataset에 대해서 학습을 수행하고, 그 다음엔 $f_2(x)$, $f_3(x)$ ... 에 대해서 학습시킨다.
그렇다면 잔차에 대해서 학습하는 것이 왜 gradient와 연관이 있을까?
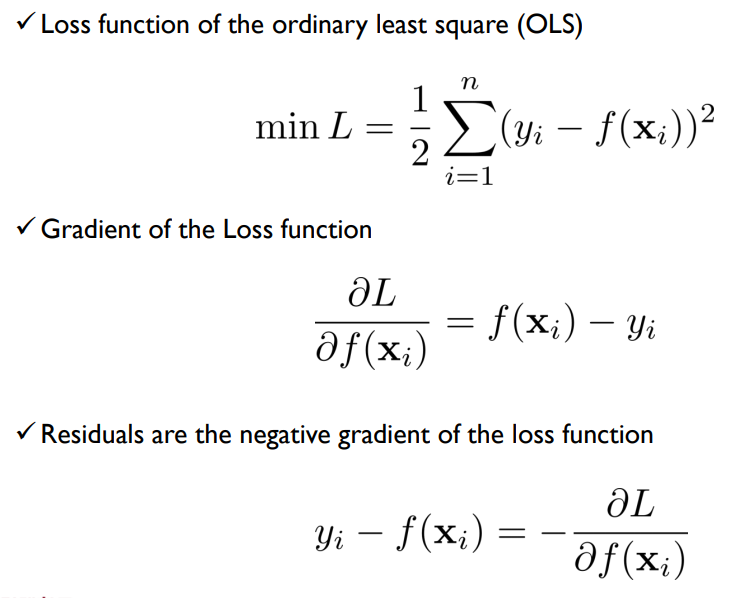
OLS 손실 함수를 $f(x)$에 대해서 미분하고 이를 정리하면 잔차가 손실함수의 gradient의 음수임을 알 수 있다. 이는 gradient의 반대 방향으로 학습시키라는 Gradient Descent 알고리즘과 유사하다.
GBM Regression Example 1
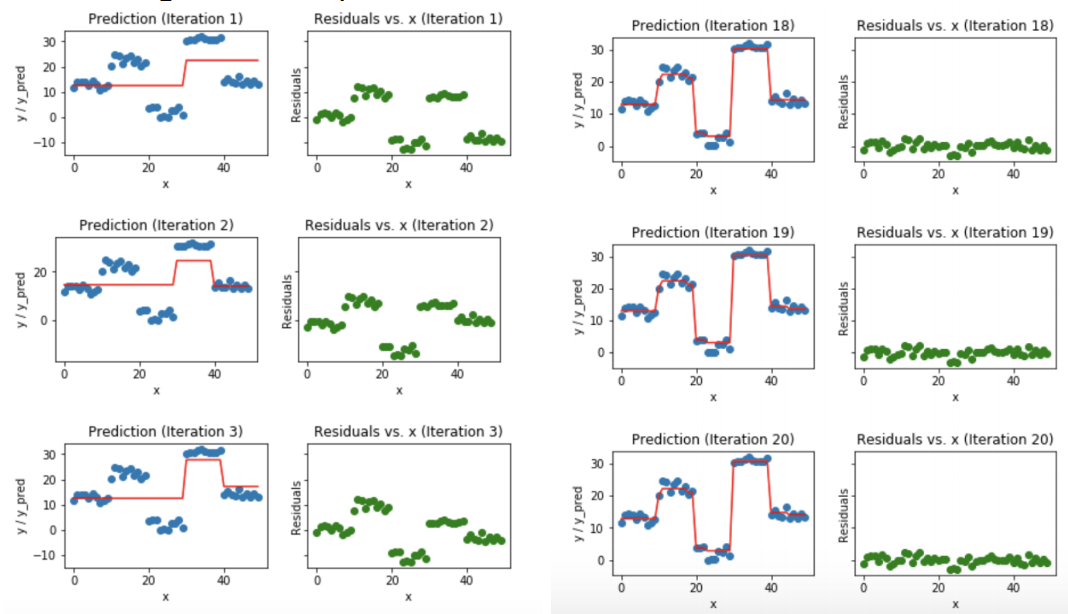
매 iteration마다 잔차에 대해 학습하는 GBM의 예시이다. 오른쪽의 초록색 점들이 잔차를 표현한 scatter이다.
잔차들이 학습을 진행할 수록 0에 근접해가는 것을 확인할 수 있다.
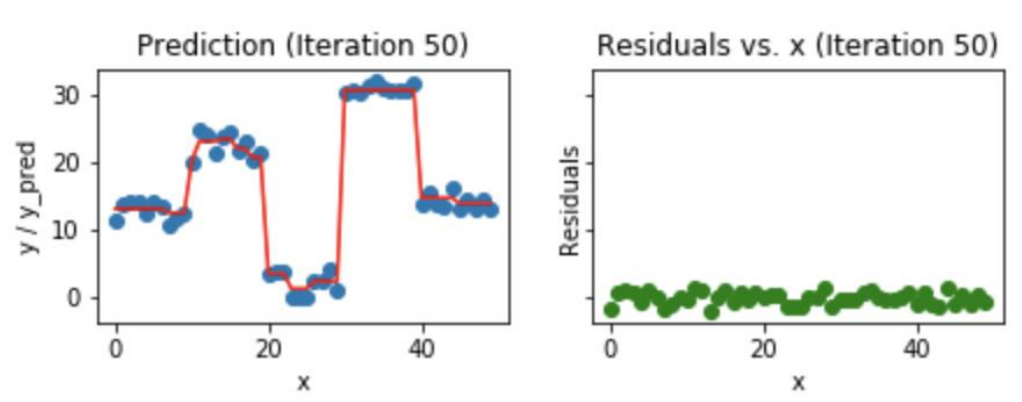
50번 째 단계의 모델이 학습한 회귀식 (빨간색 선)을 보면 잔차를 학습하느라 꼬불꼬불한 모습을 볼 수 있다. 이러한 부분 때문에 과적합이 발생하기 쉽다.
GBM Regression Example 2
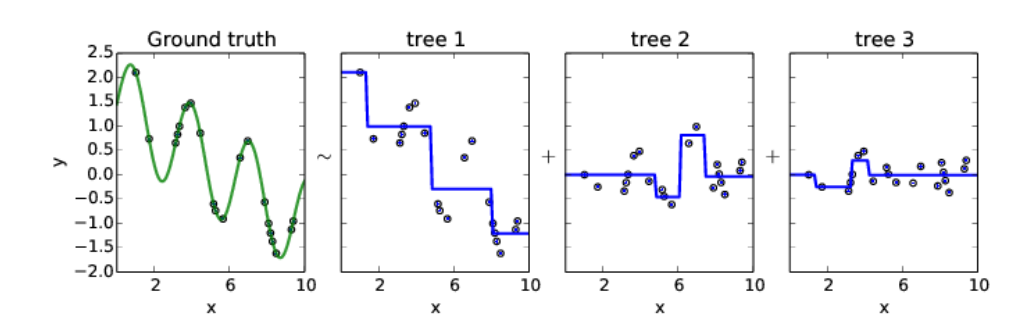
GBM 역시 base learner로 트리를 사용하는데 tree 1을 보면 split point가 3개이다. 즉, Adaboost처럼 stump tree를 사용하는 것이 아니고 depth가 2인 트리를 사용하는 것을 알 수 있다. tree 2, tree 3을 보면 original dataset의 target을 학습하는 것이 아닌 잔차를 target으로 학습하는 것을 알 수 있다.
Loss Functions for Regression
손실 함수에 따라 모델의 결과에 차이가 발생할 수 있다. 따라서 직접 학습을 시켜봄으로써 최적의 손실 함수를 선택해야 한다.

Loss Functions for Classification

Overfitting problem in GBM
앞서 한 번 언급했듯이 GBM은 과적합되기가 쉽다. 왜냐하면 잔차에 대해서 지속적으로 학습하기 때문에 noise까지 다 학습해버리기 때문이다. 이를 해결하기 위한 몇 가지 규제 방법이 있다.
Subsampling
각 단계마다 데이터의 일정 부분만 샘플링하여 사용한다. 일반적으로 subsample 비율을 float으로 표현하고 0.8이라면 전체 데이터에서 80%만 복원 추출이나 비복원 추출을 통해서 샘플링한다.
Shrinkage
후반부에 만들어진 모델들에 대해서는 영향력을 줄이는 방법이다. Original GBM이 $\hat y = f_1(x) + f_2(x) + f_3(x)$라면 shrinkage가 적용된 GBM의 예시는 $\hat y = f_1(x) + 0.9f_2(x) + {0.9}^2f_3(x)$이다.
Early Stopping
validation dataset에 대한 성능이 증가하지 않으면 학습을 중단한다.
Variable Importance in Tree-based Gradent Boosting

- $IG_i$ : i번 째 스플릿의 information gain
- $1(S_i=j)$ : i번 째 스플릿에서 변수 j를 사용했다면 1 아니면 0
- 즉, 어떤 트리를 만드는데 있어서 해당 변수를 사용한 경우의 information gain의 합이다.
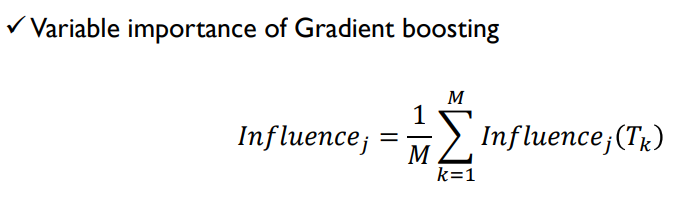
그런 다음 모든 트리에 대한 평균을 최종 변수 중요도로 사용한다.
'Machine Learning > Business Analytics 2' 카테고리의 다른 글
| 4-8 : Ensemble Learning - Light GBM (0) | 2023.12.29 |
|---|---|
| 4-7 : Ensemble Learning - XGBoost (0) | 2023.12.29 |
| 4-5 : Ensemble Learning - Adaptive Boosting (AdaBoost) (0) | 2023.12.18 |
| 4-4 : Ensemble Learning - Random Forest (0) | 2023.12.18 |
| 4-3 : Ensemble Learning - Bagging (0) | 2023.12.11 |



