Random Forest
- 반드시 base learner를 decision tree로 하는 특별한 bagging
- 2가지 방법으로 앙상블의 다양성을 증가시킨다.
- bagging
- 무작위로 선택된 예측 변수들 : p개의 예측 변수가 있다면 (p > m)을 만족하는 m개의 변수만 선택
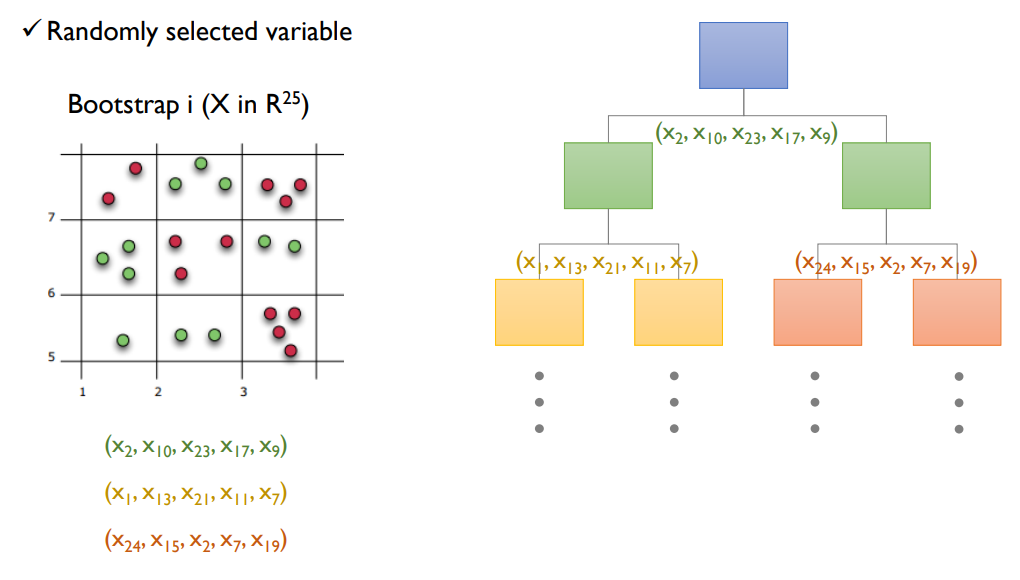
- 왼쪽은 bootstrap으로 생성된 i번 째 데이터셋이고 $x_1$ ~ $x_{25}$까지 25개의 변수를 갖고 있다.
- 오른쪽은 recursive partitioning을 표현한 것인데. 매 split point마다 random하게 선택된 변수들만 가지고 partitioning을 수행한다.
- 그러다보니 당연하게도 모든 변수를 다 사용했을 때 보다 information gain이 낮아질 수 있다.
- 그럼에도 왜 좋은지 의문이 들 수 있다. 다음 예시를 살펴보자.
1번 집단
| 국어 | 영어 | 수학 | |
| A | 70 | 80 | 89 |
| B | 70 | 80 | 90 |
| C | 70 | 80 | 91 |
2번 집단
| 국어 | 영어 | 수학 | |
| A | 95 | 60 | 60 |
| B | 60 | 95 | 60 |
| C | 60 | 60 | 95 |
1번 집단과 2번 집단을 비교해보았을 때 A, B, C 각각 개별 성적의 평균은 항상 1번 집단이 높다. 그렇지만 셋이 모여서 국영수 문제를 푼다고 가정하면 2번 집단이 최고 점수는 더 높을 것이다. 이것이 Random Forest가 추구하는 다양성이다.
정리해보자면
- Bagging으로 다양성 확보
- 변수를 선택적으로 사용한다. 즉, 변수 선택에 제약을 줌으로써 다양성 확보
Generalization Error
- Random Forest의 개별 트리는 pruning을 수행하지 않기 때문에 데이터에 과적합될지도 모른다.
- Population의 크기가 충분히 크다면 random forest의 일반화 오류는 다음과 같다.
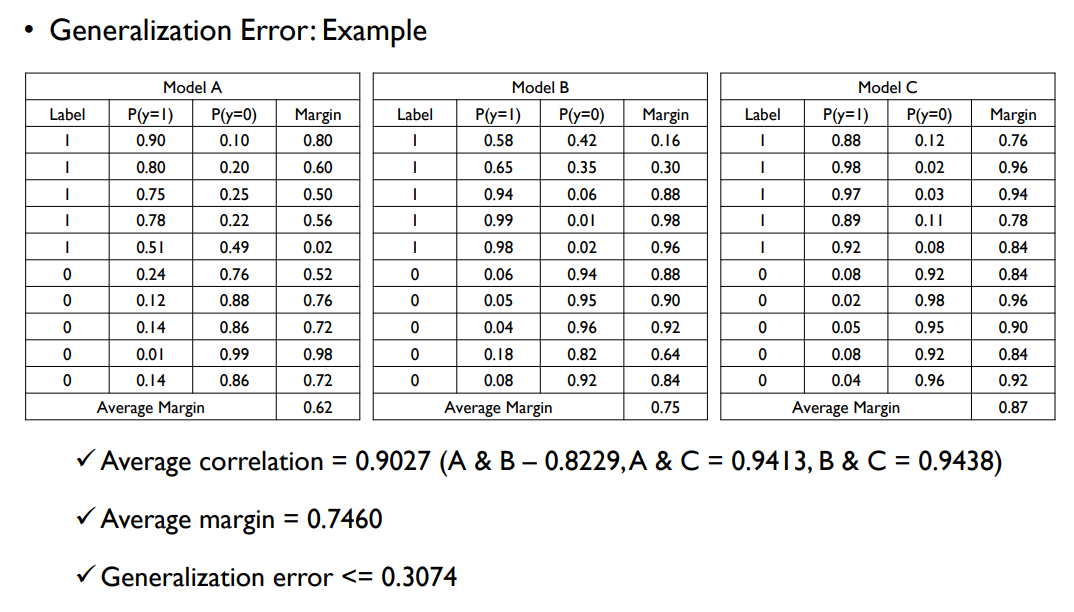
$Generalization Error \le \frac{\bar {\rho}(1-s^2)}{s^2}$
- $\bar {\rho}$ : 개별 트리간의 상관 계수의 평규
- $s^2$ : margin function (이진 분류의 경우, 정답으로 예측한 확률과 오답으로 예측한 확률의 차이의 평균)
- 정확한 개별 트리가 많을 수록 $s^2$의 값은 커지고 일반화 오류는 낮아진다.
- 트리간에 상관이 적을 수록 일반화 오류는 낮아진다.
Variable Importance
- 기존 데이터셋으로 OOB error $e_i$를 계산한다. 여기서 기존 데이터셋이란 bootstrap으로 생성된 데이터셋을 의미.
- 변수 $x_i$의 데이터를 섞은(permutation) 뒤에 OOB error $p_i$를 계산한다.
- $p_i - e_i$로부터 평균과 표준편차를 계산하여 변수 중요도를 계산한다.
만약에 $x_i$가 split에 사용되지 않았다면 $p_i = e_i$일 것이다. 그렇지만 $x_i$가 split에 자주 사용되었었다면 $p_i > e_i$이다.
랜덤 포레스트에서 변수의 중요도가 높다면
- Random permutation 전과 후의 OOB Error 차이가 크게 나타나야 하며,
- 개별 트리 마다 그 차이의 편차가 적어야 함

'Machine Learning > Business Analytics 2' 카테고리의 다른 글
| 4-7 : Ensemble Learning - XGBoost (0) | 2023.12.29 |
|---|---|
| 4-6 : Ensemble Learning - Gradient Boosting Machine (GBM) (0) | 2023.12.28 |
| 4-5 : Ensemble Learning - Adaptive Boosting (AdaBoost) (0) | 2023.12.18 |
| 4-3 : Ensemble Learning - Bagging (0) | 2023.12.11 |
| 4-2 : Ensemble Learning - Bias-Variance Decomposition (0) | 2023.12.11 |



