CNN 구현하기
MNIST 데이터를 위한 간단한 CNN을 구현한다. 구조는 다음과 같다.
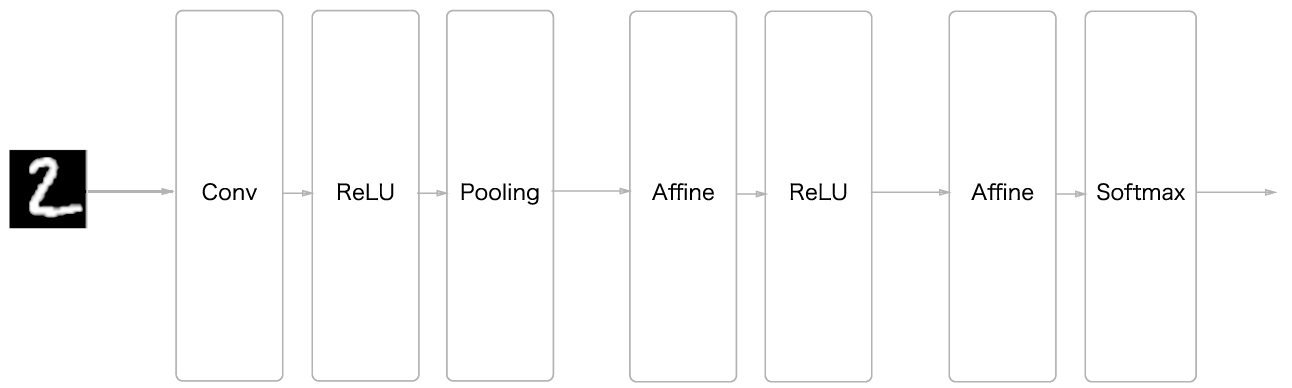
class SimpleConvNet:
def __init__(self, input_dim=(1, 28, 28),
conv_param={'filter_num':30, 'filter_size':5, 'pad':0, 'stride':1},
hidden_size=100, output_size=10, weight_init_std=0.01):
filter_num = conv_param['filter_num']
filter_size = conv_param['filter_size']
filter_pad = conv_param['pad']
filter_stride = conv_param['stride']
input_size = input_dim[1]
conv_output_size = (input_size - filter_size + 2*filter_pad) / filter_stride + 1
pool_output_size = int(filter_num * (conv_output_size/2) * (conv_output_size/2))
# 가중치 초기화
self.params = {}
self.params['W1'] = weight_init_std * \
np.random.randn(filter_num, input_dim[0], filter_size, filter_size)
self.params['b1'] = np.zeros(filter_num)
self.params['W2'] = weight_init_std * \
np.random.randn(pool_output_size, hidden_size)
self.params['b2'] = np.zeros(hidden_size)
self.params['W3'] = weight_init_std * \
np.random.randn(hidden_size, output_size)
self.params['b3'] = np.zeros(output_size)
# 계층 생성
self.layers = OrderedDict()
self.layers['Conv1'] = Convolution(self.params['W1'], self.params['b1'],
conv_param['stride'], conv_param['pad'])
self.layers['Relu1'] = Relu()
self.layers['Pool1'] = Pooling(pool_h=2, pool_w=2, stride=2)
self.layers['Affine1'] = Affine(self.params['W2'], self.params['b2'])
self.layers['Relu2'] = Relu()
self.layers['Affine2'] = Affine(self.params['W3'], self.params['b3'])
self.last_layer = SoftmaxWithLoss()- conv_output_size를 구할 땐 이전에 보았던 공식을 따른다.

다만 output의 H, W와 filter의 H, W을 통일하여 H, W는 input_size, FH, FW은 filter_size로 통일하여 계산하였다.
- pool_output_size는 affine 계층의 input_size를 구하기위해 단순히 flatten했을 경우의 뉴런 수를 계산한 것이다.
- 가중치 초기화는 간단히 표준편차가 0.01인 정규분포를 사용하였지만 ReLU 활성화 함수를 사용하므로 He 초깃값을 사용하면 결과가 더 좋을 수도 있다.
- 계층 생성은 이전과 마찬가지로 OrderDict() 클래스를 사용하여 순서를 기억하고 이를 predict와 loss계산에서 이용한다.
이밖에 predict, loss, accuracy, gradient 메서드들은 이전과 동일하다.
시간이 오래 걸려서 train 5000개, val 1000개로 학습하였다. 정확도 learning curve는 다음과 같다.

끝으로 갈수록 살짝 오버피팅되었지만 callback 까진 이 책에서 다루지 않는다....
CNN 시각화하기
학습된 필터와 학습되지 않은 필터를 시각화해보자.


학습 전에는 규칙성이 없지만, 학습을 마친 필터를 어느정도 규칙성을 가진 이미지가 되었다. 필터들은 색상이 바뀐 경계선인 엣지와 국소적으로 덩어리진 영역인 블롭 등을 보고있다.
예를 들어 가로 에지와 세로 에지에 반응하는 필터는 다음과 같다.

학습 후의 첫 번째 필터를 보면 가로 엣지에 반응하는 필터임을 알 수 있다. 각 필터들이 이미지의 국소적인 부분 부분을 인식하여 이미지를 이해하고 있는 것 같다.
층 깊이에 따른 추출 정보 변화
앞에서는 하나의 합성곱 계층을 사용헀지만 당연히 여러개 사용할 수 있다. (그치만 무조건 많다고 좋은건 아님, gradient vanishing 문제 같은 것 때문)

하위 층의 합성곱 계층은 저수준의 정보를 인식하고 상위 층으로 갈수록 고수준의 정보를 인식한다.
'책 > 밑바닥부터 시작하는 딥러닝' 카테고리의 다른 글
| 8장 딥러닝 (0) | 2023.09.22 |
|---|---|
| 7장 CNN (1) (0) | 2023.09.21 |
| 6장 학습 관련 기술들 (2) (0) | 2023.09.20 |
| 6장 학습 관련 기술들 (1) (0) | 2023.09.20 |
| 5장 오차역전파법 (2) (0) | 2023.09.19 |



