EfficientNet: Rethinking Model Scaling for Convolutional Neural Networks
1. Introduction
ResNet-18을 ResNet-200으로 확장하는 것처럼 ConvNets을 확장하여 더 나은 정확도를 달성하는 것이 일반적이다. 이 경우에는 깊이를 확장한 것인데, 너비와 이미지 해상도를 확장할 수도 있다. 그러나 문제점은 이러한 세 가지 차원을 임의로 확장할 수는 있지만, 임의로 확장하는 것은 수동 조정이 필요하며 최적의 정확도로 효율성을 얻지 못할 수 있다.
위와 같이 어떤 차원에 대해 확장하는 것은 scaling up이라고 부르는데, 저자들은 전통적인 방식과 달리 compound scaling method를 제안한다. 이는 네트워크 너비, 깊이 그리고 해상도를 일련의 고정 스케일링 계수로 균일하게 확장하는 것이다. 즉, 세 가지 차원 간의 관계를 정량화한 것으로 이해할 수 있다. Figure 2는 모델 스케일링을 시각적으로 보여준다.

이 스케일링 방법의 효과는 base 네트워크에 크게 의존하는 데, 기존의 MobileNets과 ResNet에서 잘 작동한다고 한다. 그리고 더 나아가 새로운 base 네트워크인 EfficientNets을 제안한다. EfficientNets의 모델 패밀리 중 B7은 ImageNet top-1 정확도에서 SOTA를 달성하였고, 비슷한 파라미터 개수를 가진 ResNet-50과 B4를 비교해보면 top-1 정확도를 6.7% 향상시켰다.

2. Compound Model Scaling
2.1 Problem Formulation
최적의 레이어 구조를 찾는 것이 아닌 base 네트워크는 고정시켜두고 네트워크 길이 $L_i$, 너비 $C_i$ 및 해상도 $(H_i, W_i)$ 를 확장한다. 예를 들어 ResNet의 각 스테이지는 동일한 네트워크 구조를 사용하지만 파라미터가 다르다. Base 네트워크를 고정시켜두더라고 탐색 범위가 너무 넓기 때문에 모든 레이어가 일정한 비율로 균일하게 확장되어야 한다는 제약을 부여한다. 이는 이러한 제약 조건에서 모델 정확도를 최대화하는 최적화 문제로 정의될 수 있다.

d, w, r은 각각 네트워크의 깊이, 너비, 해상도에 대한 스케일링 계수이다.
2.2 Scaling Dimension

Figure 3은 baseline 모델의 w, d, r을 달리하면서 ImageNet top-1 정확도를 나타낸 것이다. 모델은 EfficientNet B0이며 다음 섹션에서 소개한다. 결론적으로 어떤 차원을 확장하더라도 정확도가 향상되지만, 더 큰 모델일수록 정확도 향상이 줄어든다.
2.3 Compound Scaling
직관적으로, 더 높은 해상도 이미지의 경우 네트워크의 깊이나 너비를 증가시키는 것이 특징을 포착하는 데 도움이 될 것이다.
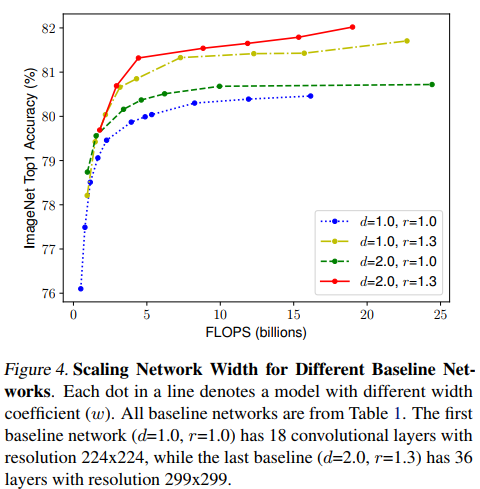
Figure 4의 각 점은 각각 다른 w를 갖고 있다. 즉 d, r을 고정시켜두고 w만 증가시키면 정확도가 금방 포화되지만, 파란색과 빨간색을 비교해보면 더 깊고, 더 높은 해상도에서 동일한 FLOPS 비용으로 width 스케일링이 더 나은 정확도를 달성한다. 따라서 너비, 깊이 및 해상도의 모든 차원을 균형 있게 조정하는 것이 중요하다.

d, w, r은 위 수식에 의해 결정된다. $\phi$는 모델 스케일링에 사용가능한 추가 리소스가 얼마나 많은지를 제어하는 사용자 지정 계수이다. 이 논문에서는 $\alpha \cdot {\beta}^2 \cdot {\gamma}^2$ 값을 약 2로 고정하는 제한을 걸어두고 최적의 조합을 찾는다.
3. EfficientNet Architecture
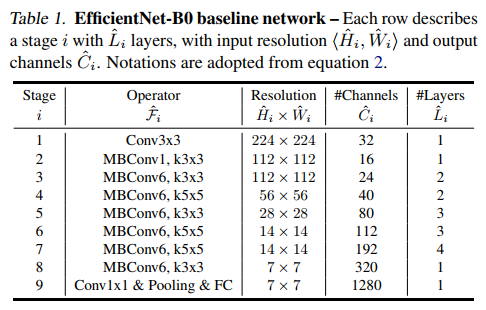
Table 1은 B0의 구조를 보여준다. MBConv는 mobile inverted bottleneck convolution을 의미한다. 저자들은 정확도와 FLOPS를 둘 다 최적화 하기 위해 목적 함수를 $ACC(m) \times [FLOPS(m)/T]^w$으로 설정했다. m은 모델, T는 타겟 FLOPS, w(=-0.07)는 ACC, FLOPS의 트레이드 오프 계수이다. 그리고 이 탐색을 통해 B0 네트워크를 개발하였다.
그런 다음 B0을 사용해 $\phi = 1$로 고정하고 그리드 서치를 통해 최적의 값을 $\alpha=1.2$, $\beta=1.1$, $\gamma=1.15$로 찾아내었다. 찾아낸 $\alpha, \beta, \gamma$값을 상수로 하고 $\phi$를 달리하면서 B1 ~ B7를 얻었다.

4. Experiments
대부분 실험 결과들이 특별한 것은 없고 우리 모델이 다른 모델보다 뛰어나다는 내용이라 CAM만 확인해보자.

Figure 7을 보면 모델에 compound scaling method를 적용했을 때 더 관련성 있는 영역에 초점을 맞추는 경향이 있음을 알 수 있다.



