Sharpness-Aware Minimization for Efficiently Improving Generalization
Google Research에 계시는 분들이 ICLR 2021에 게재한 논문이다.
1. Introduction
현대의 ML, DL은 성능을 끌어올리기 위해 overparameterization이 되어있다. 그렇지만 이는 overfitting에 취약하고 train 데이터를 단순히 memorization하는 문제점이 있다. 이런 경우에는 모델이 train 데이터를 떠나서 population distribution에 대해 일반화가 잘 된 모델인지 생각해 볼 필요가 있다.
일반적으로 모델을 훈련시키기 위해서는 mse나 cross entropy처럼 단순한 손실 함수를 사용하는데, 이는 non-convex loss landscape를 만들어 낼 가능성이 있다. 그리고 non-convex loss landscape에서는 여러 개의 local minima가 존재할 가능성이 높아 알고리즘이 local minima에 수렴할 위험이 있다. 반면에 convex한 경우에는 유일한 global minima가 존재하여 일반화 성능을 높일 수 있다.
현재 사용하는 solution으로는 Adam, RMSProp과 같이 적절한 optimizer를 선택하는 방법이 있는데, 이것이 일반화와 어떤 관계가 있는지는 생각해 볼 필요가 있다. 그리고 batch normalization, dropout, stochastic depth 등과 같이 training process를 수정하는 시도가 있다.
non-convex minimum 즉 sharp minimum이 문제가 되는 이유는 다음 그림으로 이해할 수 있다.

위 그림은 parameter에 대한 loss function을 나타낸다. sharp minimum 지점의 parameter를 선택하고 이를 test 데이터에 적용해보면 loss의 차이가 매우 큼을 알 수 있고(y축에 수직인 직선을 그었을 때 빨간 점선과 만나는 지점을 생각해보자) 이는 곧 일반화 성능이 떨어지는 것을 알 수 있다. 반면에 flat minimum의 경우에는 약간의 차이는 있지만 일반화 성능에는 큰 차이가 없다.
따라서 저자들은 loss landscape geometry를 사용하여 모델 일반화를 수행할 수 있는 효율적이고 효과적인 SAM을 제안한다. SAM의 특징은 다음과 같다.
- training loss와 loss sharpness를 둘 다 최소화한다.
- fine-tuning과 trained from scratch 두 경우 모두 일반화 성능을 향상시킨다.
- noisy label에 대해 강건하다
- m-shrpness라는 새로운 개념을 제시한다.


왼쪽 그림은 optimizer로 SGD를 사용해 훈련한 ResNet의 loss landscape이다. 그림에서 볼 수 있듯이 sharp minimum을 갖고 있고, 이 외에도 다수의 local minima가 존재한다. 반면에 논문에서 제안한 SAM을 사용해 훈련한 ResNet의 loss landscape는 convex하고 유일한 global minima가 존재한다.

위 그림은 SAM을 적용하되 모델과 데이터 증강을 다르게 하면서 여러 벤치마크 데이터셋에 대한 에러 감소율을 나타낸 것인데, 거의 모든 경우에서 많은 에러를 감소시켰다.
2. Sharpness-Aware Minimization
Notation 정리
- scalar $a$, vector $\mathbf{a}$, matrix $ \mathbf{A} $, set $\mathcal{A}$
- model parameter $ \mathbf{w} $
- loss function $l$
- training loss $L_S(\mathbf{w})$
- population loss $L_D(\mathbf{w})$
학습의 목표는 $L_D(\mathbf{w})$을 최소화하는 $\mathbf{w}$를 찾되, $\mathbf{w}$의 전체 이웃들도 모두 낮은 training loss를 가져야 한다. 그래야 해당 $\mathbf{w}$에서 convex한 loss landscape가 생기기 때문이다.
저자들은 PAC bayesian upper bound을 이용해 $\rho > 0$에 대해서 $L_D(\mathbf{w})$의 upper bound를 다음과 같이 정리하였다.

$h$는 단조 증가 함수이다. 여기서 $w + \epsilon$이 의미하는 것이 $w$의 이웃들이다. 즉 우변의 왼쪽 term은 반경이 $\rho$인 $ \epsilon $중에서 training loss가 가장 큰 값을 의미한다. 수식 1을 다시 정리하면 다음과 같다.

대괄호가 씌워진 부분이 $\mathbf{w}$에 대한 training loss의 sharpness한 정도로 이해할 수 있다. 즉 이 값이 크면 non-convex 한것이고 작으면 convex하다. 다음과 같이 그림으로 쉽게 이해할 수 있다.
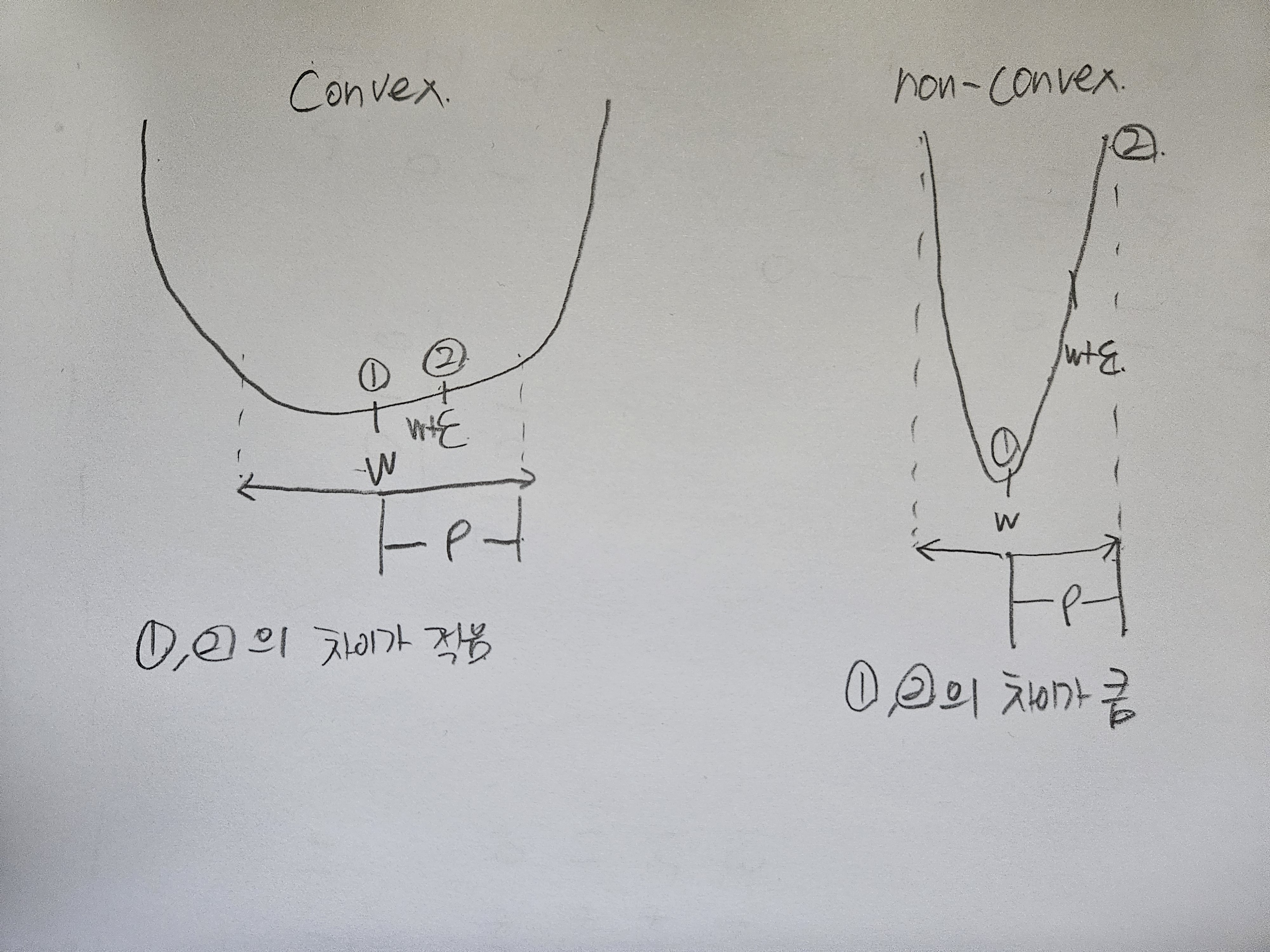
$h$ term을 L2 정칙화로 대체하면 SAM을 다음과 같이 정의할 수 있다.
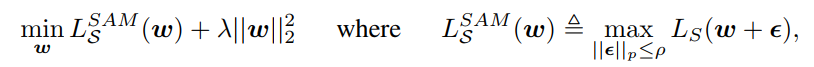
$L_S^{SAM}(w)$을 최소화하기 위해 gradient를 계산하려면 오른쪽에 max 수식의 gradient를 구해야한다. 따라서 max를 근사해야한다. 저자들은 이를 위해 1차 taylor expansion을 사용하였다.
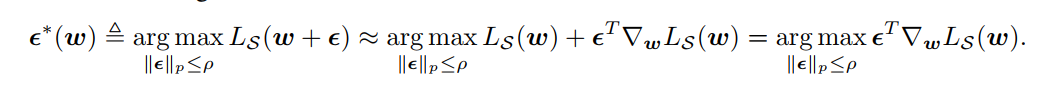
수식4를 만족하는 $\epsilon$은 다음과 같이 dual norm을 적용하여 자명하게 구할 수 있다고 합니다. (사실 이해가 잘 안됨)
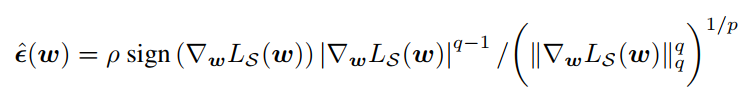
이제 수식3의 오른쪽에서 max를 지울 수 있으니 $\epsilon$ 대신 $\hat {\epsilon}$을 넣어서 미분하면 다음과 같다.
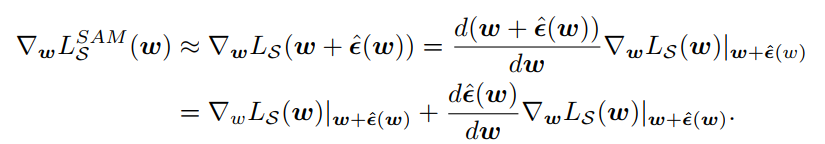
수식 6의 오른쪽 term은 hessian matrix이다. hessian은 변수의 개수에 따라서(신경망의 parameter는 몇 천만개 이상이니까) 기하급수적으로 커지기 때문에 연산 속도를 위해 drop하고 최종적으로 다음과 같이 근사할 수 있다.
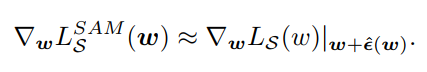
base optimizer로 SGD를 사용한 SAM 알고리즘을 의사 코드로 나타내면 다음과 같다.

- base optimizer를 사용해 배치에 대한 training loss를 구한다.
- 수식 2에 의해 $\hat {\epsilon}$을 계산한다.
- 수식 3으로 최종적인 gradient를 근사한다.
3. 코드 구현
import torch
class SAM(torch.optim.Optimizer):
def __init__(self, params, base_optimizer, rho=0.05, adaptive=False, **kwargs):
assert rho >= 0.0, f"Invalid rho, should be non-negative: {rho}"
defaults = dict(rho=rho, adaptive=adaptive, **kwargs)
super(SAM, self).__init__(params, defaults)
self.base_optimizer = base_optimizer(self.param_groups, **kwargs)
self.param_groups = self.base_optimizer.param_groups
self.defaults.update(self.base_optimizer.defaults)
@torch.no_grad()
def first_step(self, zero_grad=False):
grad_norm = self._grad_norm()
for group in self.param_groups:
scale = group["rho"] / (grad_norm + 1e-12)
for p in group["params"]:
if p.grad is None: continue
self.state[p]["old_p"] = p.data.clone()
e_w = (torch.pow(p, 2) if group["adaptive"] else 1.0) * p.grad * scale.to(p)
p.add_(e_w) # climb to the local maximum "w + e(w)"
if zero_grad: self.zero_grad()
@torch.no_grad()
def second_step(self, zero_grad=False):
for group in self.param_groups:
for p in group["params"]:
if p.grad is None: continue
p.data = self.state[p]["old_p"] # get back to "w" from "w + e(w)"
self.base_optimizer.step() # do the actual "sharpness-aware" update
if zero_grad: self.zero_grad()
@torch.no_grad()
def step(self, closure=None):
assert closure is not None, "Sharpness Aware Minimization requires closure, but it was not provided"
closure = torch.enable_grad()(closure) # the closure should do a full forward-backward pass
self.first_step(zero_grad=True)
closure()
self.second_step()
def _grad_norm(self):
shared_device = self.param_groups[0]["params"][0].device # put everything on the same device, in case of model parallelism
norm = torch.norm(
torch.stack([
((torch.abs(p) if group["adaptive"] else 1.0) * p.grad).norm(p=2).to(shared_device)
for group in self.param_groups for p in group["params"]
if p.grad is not None
]),
p=2
)
return norm
def load_state_dict(self, state_dict):
super().load_state_dict(state_dict)
self.base_optimizer.param_groups = self.param_groups
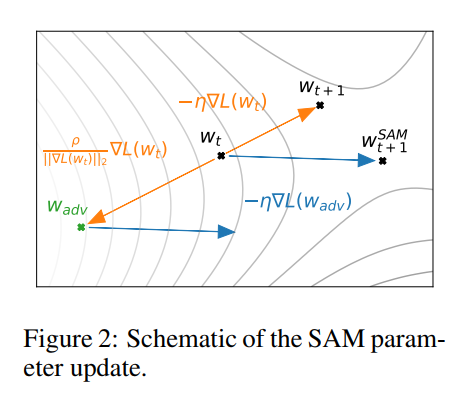
- first_step에서 $w_t$를 $w_{adv}$로 보내는 역할을 한다. 이것이 파라미터를 일시적으로 local maximum으로 올려서 sharpness를 완화시킨다. 이 과정에서 gradient가 달라진다. 즉 원래는 주황색 선을 따라 $w_{t + 1}$로 업데이트 된다면, 이 과정을 통해 파란색 선을 따라 업데이트하게 된다. 구현 코드에서는 step 메서드의 closure()를 호출하여 손실 함수의 값을 계산하고 gradient를 구한다.
- second_step에서는 이전에 저장해둔 파라미터 값을 다시 현재 파라미터로 할당하여 실제 최적화 알고리즘을 사용하여 마라티러를 업데이트한다.
'논문 리뷰' 카테고리의 다른 글
| [논문 리뷰] Swin Transformer V2 (0) | 2024.05.02 |
|---|---|
| [논문 리뷰] SRGAN (0) | 2024.04.23 |
| [논문 리뷰] Self-training with Noisy Student improves ImageNet classification (0) | 2024.04.20 |
| [논문 리뷰] EfficientNet: Rethinking Model Scaling for Convolutional Neural Networks (0) | 2024.04.19 |
| [논문 리뷰] Sentence-BERT: Sentence Embeddings using Siamese BERT-Networks (0) | 2024.03.29 |



