Swin Transformer: Hierarchical Vision Transformer using Shifted Windows
1. Introduction
Transformer의 언어 도메인에서의 높은 성능을 vision 도메인으로 전이하는데 있어 2가지 challenges가 있다.
scale의 차이
- word token과 비교하여 visual elements는 scale에서 차이가 있다.
- token이 고정된 scale을 가지고 있어 vision 응용에 적합하지 않다.
단어에 비해 이미지는 너무 고해상도 pixel을 가지고 있다.
- pixel level에서 sementic segmentation 작업 같은 dense prediction은 적합하지 않다.
- self attention의 복잡도가 이미지 크기에 대해 2차적이기 때문
이를 해결하기 위해 저자들은 이미지 크기에 대해 선형 계산 복잡도를 가지며, 계층적 특징 맵 구조를 가진 Swin Transformer를 제안한다.

Figure 1. (a)는 Swin Transformer의 계층적 구조를 보여준다. 빨간색 라인으로 구분된 영역을 local window라고 부르고 회색 라인으로 구분된 영역을 패치라고 부른다. 층이 깊어질수록 패치를 병합하는데 이 구조는 FPN, U-Net과 유사하다. 각 window의 패치의 개수는 고정된다. 또한 self attention을 local window에서만 수행하기 때문에 선형 계산 복잡도를 가질 수 있다.
핵심 설계 요소

연속적인 self attention 레이어간의 window 분할을 이동한다. 이는 이전 window의 경계를 넘어 이전 window간의 연결을 제공한다.
2. Related Work
Self attention based backbone architectures
ResNet의 일부 또는 전체 공간 합성곱 레이러를 self attention 레이어로 대체를 시도한 작업이 있었다. 성능은 ResNet보다 약간 더 나았지만, 비용이 많이 드는 메모리 액세스로 인해 실제 latency는 합성곱 네트워크보다 훨씬 크다.
Self-attention/Transformers to complement CNNs
다른 작업은 self attention 레이어나 transformer로 표준 CNN 구조를 확장하는 시도였다. Self attention 레이어로 백본이나 헤드를 보완하거나, object detection 및 segmentation 작업에 transformer의 인코더-디코더 디자인을 활용하였다. 저자들은 본인들의 연구는 기본적인 시각적 특징 추출을 위해 transformer를 활용하는 것이라고 한다.
Transformer based vision backbones
ViT의 이미지 분류 결과는 훌륭하지만, intro에서 설명했듯이 dense prediction에는 적합하지 않다. 그래서 다른 연구에서는 ViT 모델을 직업 upsampling이나 deconvolution을 통해 dense prediction에 응용하였는데 낮은 성능을 보였다.
저자들은 경험적으로 Swin Transformer 구조가 이미지 분류에서 최적의 속도-정확도 트레이드오프를 달성한다는 것을 발견했고, 특히 분류가 아닌 일반적인 성능에 중점을 두고 있다고 한다. 여러 작업으로 transfer learning이 가능한 backbone 모델을 구축하는 것이 목표인 것 같다. COCO object detection과 ADE20K sementic segmentation에서 SOTA를 달성했다고 한다.
3. Method
3.1 Overall Architecture

Figure 3. (a)는 tiny 버전인 Swin-T의 구조를, (b)는 하나의 Swin Transformer Block의 구조를 보여준다.
먼저 입력 이미지는 Patch Partition에 의해 패치들로 분할된다. 각 패치들은 token으로 부른다. 저자들은 패치의 크기를 4x4로 사용했기 때문에 각 패치의 특징 차원은 48(=4x4x3)이 된다. 그런 다음 C로 표기한 임의의 차원으로 투영하는 선형 임베딩 레이어가 적용된다. C의 값은 모델의 버전마다 차이가 있다. Swin-T의 경우는 96(=C)이다.
그런 다음 몇 개의 block을 지나게 되는데 stage 1에서는 token의 개수 (H/4 x W/4)가 유지된다.
계층적 표현을 만들기 위해서 stage 2, 3, 4에는 앞에 Patch Merging 모듈이 있다. 이웃하는 2x2 패치들을 병합함으로써 패치의 개수는 4배 줄어들며, 해상도 측면에서는 2배 다운샘플링되는 것과 동일하다.
블록이나 stage를 사용하는 측면에서 ResNet의 구조와 매우 유사해보인다.
Swin Transformer block
(b)를 보면 Block은 shifted window을 계산하기 위한 multi-head self attention(MSA)와 GELU 활성화 함수가 적용된 MLP 모듈로 구성된다. LayerNorm(LN)은 MSA와 MLP 모듈 이전에 적용되며, residual connection은 각 모듈 이후에 적용된다.
3.2 Shifted Window based Self Attention
Self-attention in non-overlapping windows
각 window가 MxM개의 패치를 포함한다고 가정하면, 이미지 hxw에 대한 global MSA와 window 기반 MSA의 계산 복잡성은 다음과 같다.
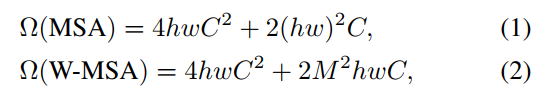
위 수식을 보면 global MSA의 경우 이미지 크기(hw)에 이차 계산 복잡도를 가지는 것을 확인할 수 있다.
Shifted window partitioning in successive blocks
Window 이동 방법에 대해 이해하기 위해 Figure 2를 다시 보자.
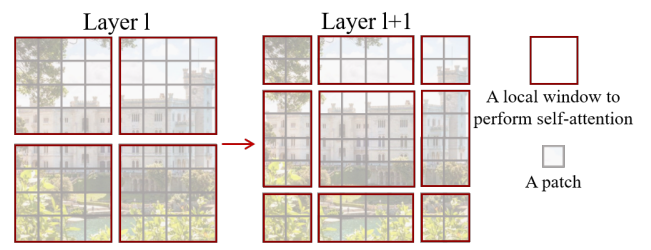
첫 번째 모듈은 정상적인 window 분할을 수행하며 8x8 특성 맵이 4x4 크기의 2x2 window로 균등하게 분할된다. 여기서 M=4인데 왼쪽을 (M/2, M/2) 만큼 평행 이동 시켜 다음 window 분할을 구성한다.
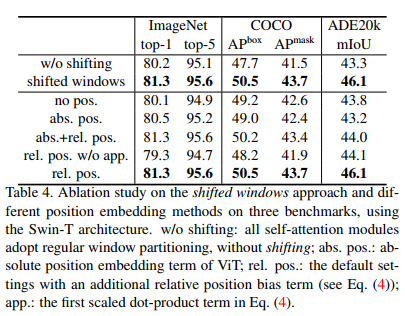
Table 4의 윗 부분을 보면 w/o shifting은 정상적인 window 분할을 나타내는데 shifted window가 이미지 분류, object detection, dense prediction에서 더 높은 성능을 보임을 확인할 수 있다.
Efficient batch computation for shifted configuration
Fig 2를 보면 shifted window로 인해 더 많은 window가 생기고 일부 window는 MxM 보다 작다. 단순한 방법은 작은 window 를 MxM으로 패딩하는 것이지만 이는 계산 증가가 상당하다. 그래서 저자들은 다음 그림과 같은 방법을 제안한다.
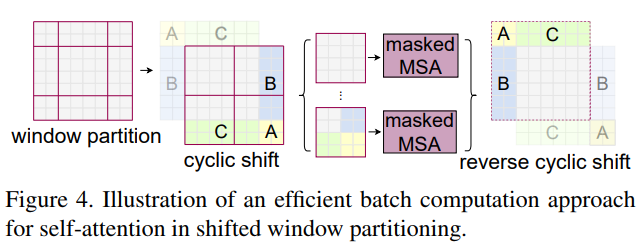
위 그림과 같이 이동 후에 각 하위 window 내에세만 self attention이 계산되도록 masking 메커니즘을 사용한다.
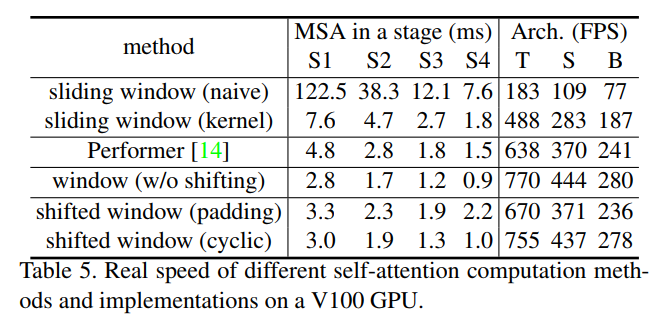
Table 5의 아래쪽을 보면 cyclic은 padding에 비해 속도가 훨씬 빠르다. 정상적인 window 분할보다 약간 느리지만 성능이 더 우수하기에 약간은 감안하는 것 같다.
Relative position bias
절대 위치 임베딩을 사용하는 대신 상대적인 위치 편향 B∈RM2×M2을 self attention 계산에 추가한다.
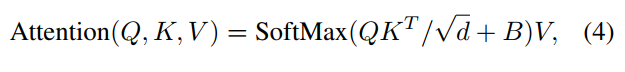
상대적인 위치의 범위는 [-M + 1, M - 1]이다. 범위가 왜 이러냐면, 예를 들어 M=2인 2x2 window를 생각해보자. window 격자를 행렬처럼 생각했을 때 (0, 0) 위치의 패치 a와 (1, 1) 위치의 패치 b에 대해서 생각해보면 a를 기준으로 b의 위치는 (+1, +1)이다. 반대로 b를 기준으로 a의 위치를 생각해보면 (-1, -1)이다. 따라서 상대적인 위치의 범위가 [-M + 1, M - 1]이 된다.
B의 값은 사전 학습된 ˆB∈R(2M−1)×(2M−1)로부터 가져온다. M=2를 대입하면 3x3크기의 행렬 ˆB로 부터 값을 가져온다. 값을 가져올 때는 인덱스를 (0, 2)와 같은 방법으로 가져오지 않고 ˆB을 flatten하여 0~8의 인덱스로 가져온다.
코드로 상대적인 위치 인덱스를 계산하는 방법을 알아보자. 다음과 같은 2x2 window가 있고 숫자는 패치의 인덱스를 의미한다. 코드는 논문의 github에서 참고하였다.
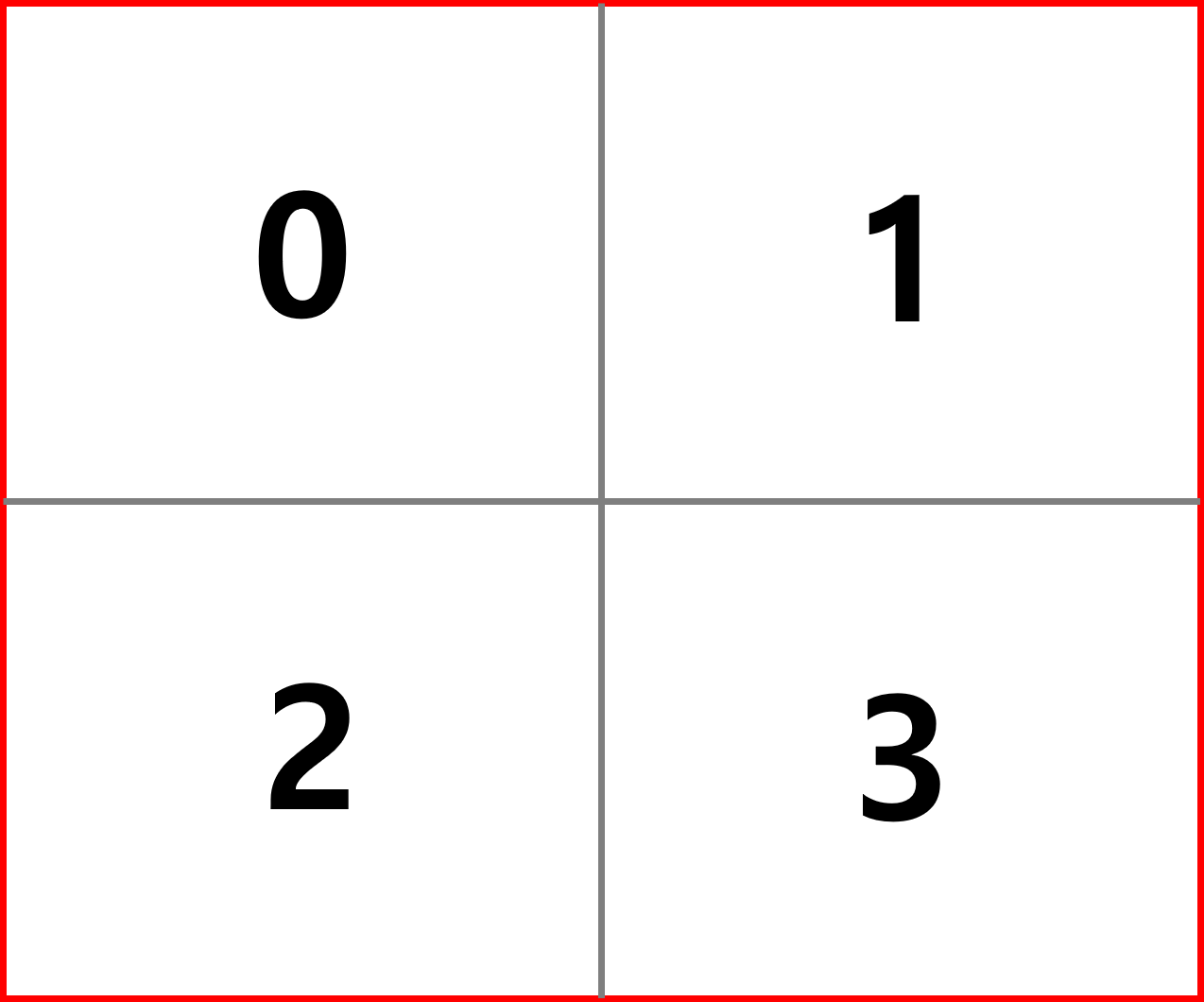
window_size = 2
coords_h = torch.arange(window_size)
coords_w = torch.arange(window_size)
coords = torch.stack(torch.meshgrid([coords_h, coords_w], indexing="ij"))
coords_flatten = torch.flatten(coords, 1)
relative_coords = coords_flatten[:, :, None] - coords_flatten[:, None, :]
print(relative_coords)
print("x축에 대한 상대적인 위치\n", relative_coords[0, :, :])
print("y축에 대한 상대적인 위치\n", relative_coords[1, :, :])tensor([[[ 0, 0, -1, -1],
[ 0, 0, -1, -1],
[ 1, 1, 0, 0],
[ 1, 1, 0, 0]],
[[ 0, -1, 0, -1],
[ 1, 0, 1, 0],
[ 0, -1, 0, -1],
[ 1, 0, 1, 0]]])
x축에 대한 상대적인 위치
tensor([[ 0, 0, -1, -1],
[ 0, 0, -1, -1],
[ 1, 1, 0, 0],
[ 1, 1, 0, 0]])
y축에 대한 상대적인 위치
tensor([[ 0, -1, 0, -1],
[ 1, 0, 1, 0],
[ 0, -1, 0, -1],
[ 1, 0, 1, 0]])
x축에 대한 상대적인 위치를 보면 같은 x축에 놓여있으면 0이고, 아래로 떨어져있다면 1, 위로 떨어져 있으면 -1이된다. (0, 2)의 값을 보면 -1이다. 이는 2번 패치 기준으로 0번 패치가 위에 있기 때문이다. y축에 대한 상대적인 위치도 동일한 방법으로 계산된다.
음수로 인덱싱할 수 없기 때문에 다음과 같이 값을 보정해준다.
x_coords = relative_coords[0, :, :]
y_coords = relative_coords[1, :, :]
x_coords += window_size - 1
y_coords += window_size - 1
x_coords *= 2 * window_size - 1
print(f"X축에 대한 상대적인 위치:\n{x_coords}\n")
print(f"Y축에 대한 상대적인 위치:\n{y_coords}\n")
relative_position_index = x_coords + y_coords
print(f"X, Y축에 대한 상대적인 위치:\n{relative_position_index}")X축에 대한 상대적인 위치:
tensor([[3, 3, 0, 0],
[3, 3, 0, 0],
[6, 6, 3, 3],
[6, 6, 3, 3]])
Y축에 대한 상대적인 위치:
tensor([[1, 0, 1, 0],
[2, 1, 2, 1],
[1, 0, 1, 0],
[2, 1, 2, 1]])
X, Y축에 대한 상대적인 위치:
tensor([[4, 3, 1, 0],
[5, 4, 2, 1],
[7, 6, 4, 3],
[8, 7, 5, 4]])
relative_position_index를 보면 0~8 범위의 값을 가지는 것을 알 수 있다.
다음은 학습된 ˆB로 부터 B값을 가져오는 방법이다. 여기서는 임의로 torch.zeros로 B_hat을 설정하였다.
B_hat = torch.Tensor(
torch.zeros((2 * window_size - 1) * (2 * window_size - 1))
)
B = B_hat[relative_position_index.view(-1)]
B = B.view(
window_size * window_size, window_size * window_size
)
print(B.shape)torch.Size([4, 4])
이렇게 구해진 B를 self attention 계산에 포함한다.
위에서 보았던 Table 4를 보면 상대적인 위치 편향을 사용하는 것이 성능이 가장 우수하다.
3.3 Archtecture Variants

모델은 선형 임베딩 차원, 스테이지 별 Block의 개수에 차이를 두어 4가지가 있다. Swin-B는 base 모델이며 이는 ViT-B/Deit-B와 비슷한 계산 복잡도를 가진다. T, S, L은 B와 비교하여 계산 복잡도가 0.25, 0.5, 2이다.
4. Experiments
4.1 Image Classification on ImageNet-1K
Training data-efficient image transformers & distillation through attention
Deit 논문의 training setting과 비슷하게 Regular ImageNet-1K training의 결과는 다음과 같다.
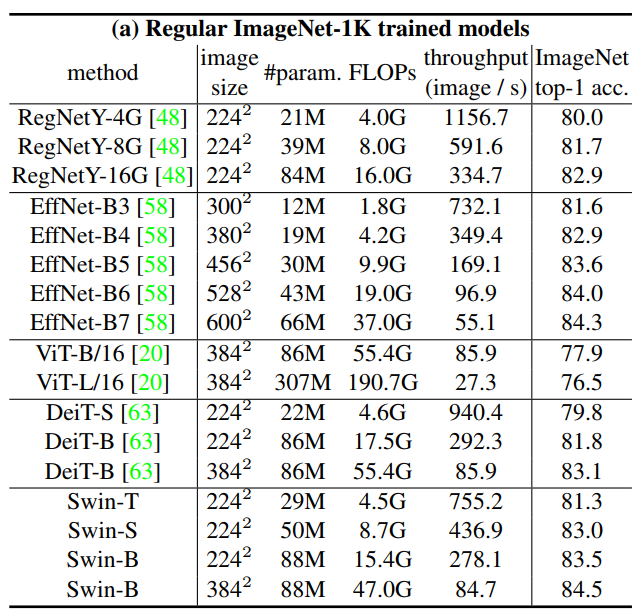
이전의 SOTA Transformer 기반의 구조와 비교하였을 때 비슷한 계산 복잡도를 가지는 경우 성능을 뚜렷하게 능가한다. 그리고 SOTA CNN 네트워크 모델인 RegNet과 EfficientNet과 비교하였을 때 약간 더 나은 속도-정확도 트레이드오프를 달성한다.
다음은 ImageNet-22K에 사전 훈련된 후 1K로 fine tuning 했을 때의 결과이다.
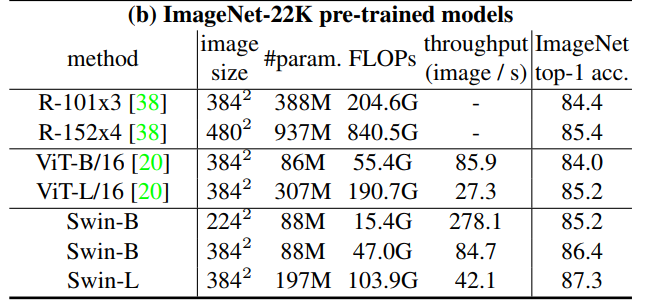
이미지 크기 384에 대해 Swin-B는 VIT-B/16과 비교하여 비슷한 추론 처리량(84.7 vs 85.9) 및 약간 낮은 연산량을 가지면서 top-1 acc가 2.4%(86.4 vs 84.0) 높다.
4.2 Object Detection on COCO
Casacade Mask R-CNN, ATSS, RepPoints v2, Sparse RCNN 프레임워크의 백본을 ResNe(X)t, DeiT, Swin Transformer로 교체해가면서 성능을 비교한다. 다만 공정한 비교를 위해 역합성 계층을 사용해 DeiT의 계층적 특징 맵을 구성하였다고 한다.
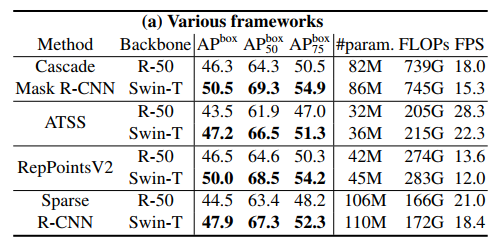
ResNet-50보다 일관된 성능 향상을 보인다.
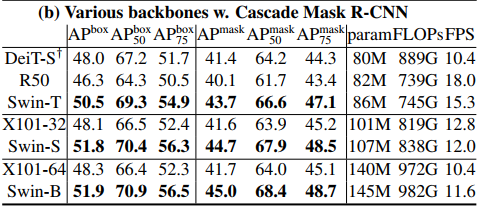
Cascade Mask R-CNN 프레임워크를 사용했을 때 비슷한 매개변수, 계산 복잡도, 추론 속도를 가진 DeiT, ResNet-101보다 더 나은 성능을 보인다.
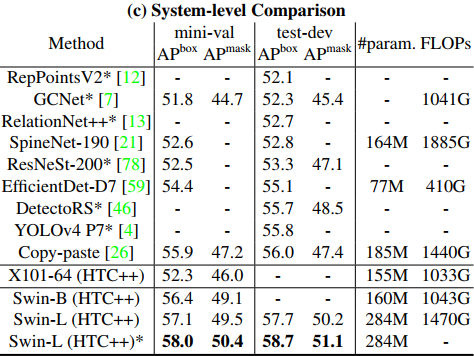
이전의 SOTA 모델들과 COCO test셋에 대해 비교하였을 때 58.8 box AP, 51.1 mask AP를 달성하며 최고 성능을 보인다.
4.3 Semantic Segmentation on ADE20K
mmseg, UperNet을 프레임워크로 사용하여 백본을 교체해가며 성능을 비교하였다.
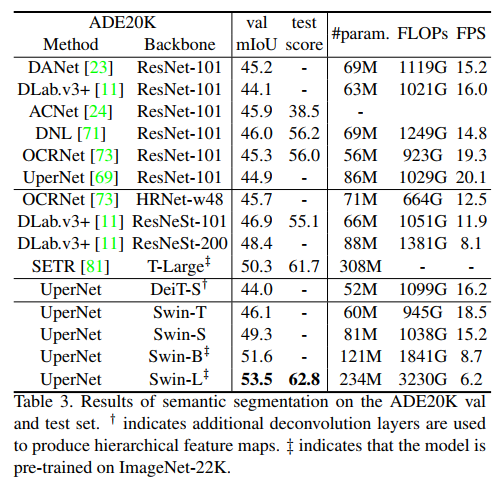
Swin-S가 유사한 계산 비용을 가진 DeiT-S보다 +5.3 mIoU 높고, ResNet-101보다 +4.4 mIoU 높다. ImageNet-22K에서 사전훈련 받은 Swin-L은 이전 SOTA 보다 +3.2 mIoU 더 높다.



